已知:如图,正方形ABCD的边长为2a,H是以BC为直径的半圆O上一点,过H与圆O相切的直线交AB于E,交CD于F.(1)当点H在半圆上移动时,切线EF在AB、CD上的两个交点也分别在AB、CD上-数学
题文
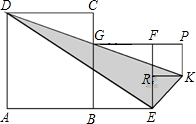
已知:如图,正方形ABCD的边长为2a,H是以BC为直径的半圆O上一点,过H与圆O相切的直线交AB 于E,交CD于F. (1)当点H在半圆上移动时,切线EF在AB、CD上的两个交点也分别在AB、CD上移动(E、A不重合,F、D不重合),试问:四边形AEFD的周长是否也在变化?证明你的结论; (2)设△BOE的面积为S1,△COF的面积为S2,正方形ABCD的面积为S,且S1+S2=
|

 ;
;
![如图,在长方形网格中,每个小长方形的长为2,宽为1,A、B两点在网格格点上,若点C也在网格格点上,以A、B、C为顶点的三角形面积为2,则满足条件的点C个数是[]A.2B.3C.4D.5-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/163/2020-05-20/facf2a6d7f4f4e42254e6c9026b6dc15.png)