等腰梯形ABCD中,AD∥BC,AB=DC=12,AD=4,∠B=60°,点P是腰AB上的一个动点.(1)求BC的长.(2)如图1,如果点M在BC上,BM=12,PM平分梯形ABCD的面积,求出此时PB的长;(3)过点P作-数学
题文
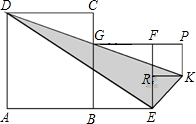
| 等腰梯形ABCD中,AD∥BC,AB=DC=12,AD=4,∠B=60°,点P是腰AB上的一个动点. (1)求BC的长. (2)如图1,如果点M在BC上,BM=12,PM平分梯形ABCD的面积,求出此时PB的长; (3)过点P作直线PM,是否存在PM将梯形ABCD的周长和面积同时平分?若存在,求出此时PB的长;若不存在,请说明理由;  |



 ;
;
![如图,在长方形网格中,每个小长方形的长为2,宽为1,A、B两点在网格格点上,若点C也在网格格点上,以A、B、C为顶点的三角形面积为2,则满足条件的点C个数是[]A.2B.3C.4D.5-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/163/2020-05-20/facf2a6d7f4f4e42254e6c9026b6dc15.png)