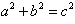已知4条线段的总长度是48cm,且第一条线段的长是acm,第二条线段比第一条线段的2倍多3cm,第三条线段的长等于第一、二两条线段的和.(1)用含a的代数式表示第四条线段的长;(2-七年级数学
题文
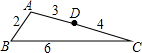
| 已知4条线段的总长度是48cm,且第一条线段的长是acm,第二条线段比第一条线段的2倍多3cm,第三条线段的长等于第一、二两条线段的和. (1)用含a的代数式表示第四条线段的长; (2)当  时,这4条线段首尾相接能构成一个四边形吗?为什么? 时,这4条线段首尾相接能构成一个四边形吗?为什么?(3)已知a为整数,如果这4条线段首尾相接能构成一个四边形,请你直接写出满足上述条件的所有a的值. |
答案
| 解:(1)∵第一条线段的长是acm,第二条线段比第一条线段的2倍多3cm,第三条线段的长等于第一、二两条线段的和, ∴第二条线段的长为(2a+3)cm, 第三条线段的长为(3a+3)cm, 第四条线段的长为(42﹣6a)cm; (2)当  时,这4条线段分别为 时,这4条线段分别为 , , ,11,26, ,11,26,∵  + + +11<26, +11<26,∴这4条线段首尾相接不能构成一个四边形; (3)满足条件的所有a的值:4,5,6. |
据专家权威分析,试题“已知4条线段的总长度是48cm,且第一条线段的长是acm,第二条线段..”主要考查你对 三角形的三边关系,写代数式 等考点的理解。关于这些考点的“档案”如下:
三角形的三边关系写代数式
考点名称:三角形的三边关系
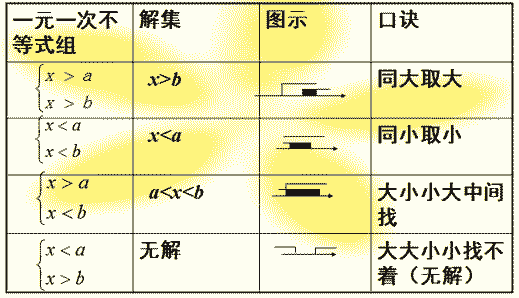
三角形的三边关系:
在三角形中,任意两边和大于第三边,任意两边差小于第三边。
设三角形三边为a,b,c
则
a+b>c
a+c>b
b+c>a
a-b<c
a-c<b
b-c<a
在直角三角形中,设a、b为直角边,c为斜边。
则两直角边的平方和等于斜边平方。
在等边三角形中,a=b=c
在等腰三角形中, a,b为两腰,则a=b
在三角形ABC的内角A、B、C所对边分别为a、b、c的情况下,c2=a2+b2-2abcosc三角形的三边关系定理及推论:
(1)三角形三边关系定理:三角形的两边之和大于第三边。
推论:三角形的两边之差小于第三边。
(2)三角形三边关系定理及推论的作用:
①判断三条已知线段能否组成三角形;
②当已知两边时,可确定第三边的范围;
③证明线段不等关系。
考点名称:写代数式
- 代数式:
由数和表示数的字母经有限次加、减、乘、除、乘方和开方等代数运算所得的式子,或含有字母的数学表达式称为代数式。
数的一切运算规律也适用于代数式。单独的一个数或者一个字母也是代数式。
例如:ax+2b,-2/3,b^2/26,√a+√2等。
带有“(≥)” “=”“≠”等符号的不是代数式
注意:
1、不包括等于号(=、≡)、不等号(≠、≤、≥、<、>、≮、≯)、约等号≈。
2、可以有绝对值。例如:|x|,|-2.25| 等。 - 代数式的书写要求:
一、数字与数字相乘时,中间的乘号不能用“? ”代替,更不能省略不写。
如:4乘5,写作4×5,不能写成4?5,更不能写成45
二、数字与字母相乘时,中间的乘号可以省略不写,并且数字放在字母的前面。
如: a的5倍,写作:5a 不要写成a5。
三、两个字母相乘时,中间的乘号可以省略不写,字母无顺序性
如: a乘b ,写成ab或ba
四、当字母和带分数相乘时,要把带分数化成假分数。
如:3 1/2 乘a 写作:7/2 a 不要写成32/1a
五、含有字母的除法运算中,最后结果要写成分数形式,分数线相当于除号。
如:5除以a 写作5/a , 不要写成5÷a ; c除以 d写作 ,不要写成 c÷ d
六、如果代数式后面带有单位名称,是乘除运算结果的直接将单位名称写在代数式后面,若代数式是带加减运算且须注明单位的,要把代数式括起来,后面注明单位。
如:甲同学买了5本书,乙同学买了a 本书,他们一共买了(5+a )本。 代数式的书写格式:
(1)数与字母,字母与字母相乘,乘号可以省略,也可写成“.”;
(2)数字要写在前面;
(3)带分数一定要写成假分数;
(4)在含有字母的除法中,一般不用“÷”号,而写成分数的形式;
(5)式子后面有单位时,和差形式的代数式要在单位前把代数式括起来。- 代数式:

- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |