题文

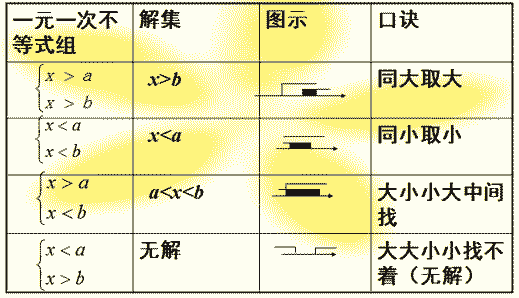
（1）用长度相等的100根火柴杆，摆放成一个三角形，使最大边的长度是最小边长度的3倍，求满足此条件的每个三角形的各边所用火柴杆的根数． （2）现有长为150cm的铁丝，要截成n（n＞2）小段，每段的长为不小于lcm的整数．如果其中任意3小段都不能拼成三角形，试求n的最大值，此时有几种方法将该铁丝截成满足条件的n段．

题型：解答题  难度：中档

答案

（1）设三角形各边需用火柴杆数目分别为x、y、3x， 依题意有 x+y+3x=100 x≤y≤3x x+y＞3x ， 由方程可得 100 7 ≤x＜ 50 3 ． 因x为正整数，故x=15或16． 所以满足条件的三角形有15，40，45或16，36，48两组； （2）这些小段的长度只可能是1，1，2，3，5，8，13，21，34，55，89… 但1+1+2+…+34+55=143＜150． 1+1+2+…+34+55+89=232＞150．故n的最大值为10，共有以下7种形式：（1，1，2，3，5，8，13，21，34，62）（1，1，2，3，5，8，13，21，35，61）（1，1，2，3，5，8，13，21，36，60）（1，1，2，3，5，8，13，21，37，59）（1，1，2，3，5，8，13，21，35，60）（1，1，2，3，5，8，13，21，36，59）（1，1，2，3，5，8，13，21，36，58）．

据专家权威分析，试题“（1）用长度相等的100根火柴杆，摆放成一个三角形，使最大边的长度..”主要考查你对  三角形的三边关系  等考点的理解。关于这些考点的“档案”如下：

三角形的三边关系

考点名称：三角形的三边关系

• 三角形的三边关系：
  在三角形中，任意两边和大于第三边，任意两边差小于第三边。
  设三角形三边为a,b,c
  则
  a+b>c
  a+c>b
  b+c>a
  a-b<c
  a-c<b
  b-c<a
  在直角三角形中，设a、b为直角边，c为斜边。
  则两直角边的平方和等于斜边平方。
  在等边三角形中，a=b=c
  在等腰三角形中， a,b为两腰，则a=b
  在三角形ABC的内角A、B、C所对边分别为a、b、c的情况下，c²=a²+b²-2abcosc

• 三角形的三边关系定理及推论：
  （1）三角形三边关系定理：三角形的两边之和大于第三边。
  推论：三角形的两边之差小于第三边。
  （2）三角形三边关系定理及推论的作用：
  ①判断三条已知线段能否组成三角形；
  ②当已知两边时，可确定第三边的范围；
  ③证明线段不等关系。