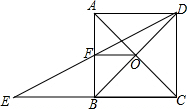
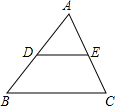
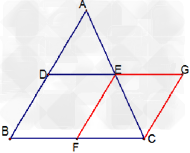
如图①在△ABC中,AE=EB,AF=FC,则EF与BC存在以下关系:EF∥BC,;将AC沿BC方向平移到DH,得图②沿CB方向平移到DH得图③图②中AD与BH存在关系:EF∥AD,;,那么在图③中是否有类似于-九年级数学
题文
如图①在△ABC中,AE=EB,AF=FC,则EF与BC存在以下关系:EF∥BC, ;将AC沿BC方向平移到DH,得图②沿CB方向平移到DH得图③图②中AD与BH存在关系:EF∥AD, ;将AC沿BC方向平移到DH,得图②沿CB方向平移到DH得图③图②中AD与BH存在关系:EF∥AD, ;,那么在图③中是否有类似于图①②中的结论,请把猜想的结论填在方框内,并就图③的结论加以证明. ;,那么在图③中是否有类似于图①②中的结论,请把猜想的结论填在方框内,并就图③的结论加以证明. |
 |
答案
| 解:(1)理由如下:延长EF到点D,使FD=EF, 在△AEF与△CDF中,  , ,∵△AEF≌△CDF(SAS), ∴AE=DC,∠D=∠AEF, ∴CD∥AB, ∵AE=EB, ∴DC=EB, ∴四边形BCDE是平行四边形, ∴ED∥BC,且ED=BC, ∴EF∥BC,且EF=  BC; BC;(2)如图②所示,根据(1)得,EG∥BC,且EG=  BH, BH,根据题意得,AD∥BC,CD∥AH, ∴四边形ADCH是平行四边形, ∵EG∥BC, ∴FG=  (AD+CH), (AD+CH),∴EF=EG﹣FG=  BH﹣ BH﹣ (AD+CH)= (AD+CH)= (BH﹣CH)﹣ (BH﹣CH)﹣ AD= AD= (BC﹣AD); (BC﹣AD);如图③所示,根据(1)得,EG∥BC,且EG=  BH, BH,根据题意得,AD∥BC,CD∥AH, ∴四边形ADCH是平行四边形, ∵EG∥BC, ∴FG=  (AD+CH), (AD+CH),∴EF=EG+FG=  BH+ BH+ (AD+CH)= (AD+CH)= (BH+CH)+ (BH+CH)+ AD= AD= (BC+AD). (BC+AD). |
据专家权威分析,试题“如图①在△ABC中,AE=EB,AF=FC,则EF与BC存在以下关系:EF∥BC,;将..”主要考查你对 三角形中位线定理,平行四边形的性质,平行四边形的判定,平移 等考点的理解。关于这些考点的“档案”如下:
三角形中位线定理平行四边形的性质平行四边形的判定平移
考点名称:三角形中位线定理
- 三角形中位线定义:
连接三角形两边中点的线段叫做三角形的中位线。一个三角形共有三条中位线。
三角形中位线定理:
三角形的中位线平行于第三边,并且等于它的一半。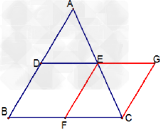
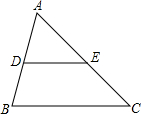
如图已知△ABC中,D,E分别是AB,AC两边中点。
则DE平行于BC且等于BC/2 - 三角形中位线逆定理:
逆定理一:在三角形内,与三角形的两边相交,平行且等于三角形第三边一半的线段是三角形的中位线。
如图DE//BC,DE=BC/2,则D是AB的中点,E是AC的中点。
逆定理二:在三角形内,经过三角形一边的中点,且与另一边平行的线段,是三角形的中位线。
如图D是AB的中点,DE//BC,则E是AC的中点,DE=BC/2 - 区分三角形的中位线和中线:
三角形的中位线是连结三角形两边中点的线段;
三角形的中线是连结一个顶点和它的对边中点的线段。
考点名称:平行四边形的性质
- 平行四边形的概念:
两组对边分别平行的四边形叫做平行四边形。
平行四边形用符号“□ABCD,如平行四边形ABCD记作“□ABCD”,读作ABCD”。
①平行四边形属于平面图形。
②平行四边形属于四边形。
③平行四边形中还包括特殊的平行四边形:矩形,正方形和菱形等。
④平行四边形属于中心对称图形。 平行四边形的性质:
主要性质
(矩形、菱形、正方形都是特殊的平行四边形。)
(1)如果一个四边形是平行四边形,那么这个四边形的两组对边分别相等。
(简述为“平行四边形的两组对边分别相等”)
(2)如果一个四边形是平行四边形,那么这个四边形的两组对角分别相等。
(简述为“平行四边形的两组对角分别相等”)
(3)如果一个四边形是平行四边形,那么这个四边形的邻角互补
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:用刻度尺找出如图中四边形ABCD各边中点E,F,G,H,再依次把它们连接起来,借助量角器等工具找一找,其中有平行直线吗?若有,是哪几对?-七年级数学
下一篇:如图,要测量A、B两点间距离,在O点打桩,取OA的中点C,OB的中点D,测得CD=30m,则AB=()m.-九年级数学
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |