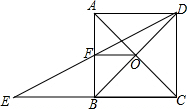
如图,AD为边BC边上中线,E为AD的中点,连BE交AC于F,则AF:AC=______(1)若AE:ED=1:2,则AF:AC=______;(2)若AE:ED=1:3,则AF:AC=______,并证明.(3)若AE:ED=1:n,猜想AF:AC=-数学
题文
| 如图,AD为边BC边上中线,E为AD的中点,连BE交AC于F,则AF:AC=______ (1)若AE:ED=1:2,则AF:AC=______; (2)若AE:ED=1:3,则AF:AC=______,并证明. (3)若AE:ED=1:n,猜想AF:AC=______.  |


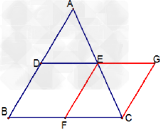
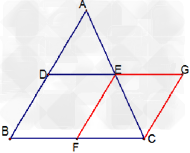
 ,则有
,则有 。
。


 ,则有
,则有 。
。


 ,则有
,则有 。
。
 ,则
,则 ,
,