题文

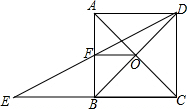
如图，等腰梯形ABCD中，AD∥BC，点E是线段AD上的一个动点（点E不与A、D重合），G、H、F分别是B E、CE和BC的中点． （1）猜想四边形EGFH的形状，并说明理由． （2）当点E运动到什么位置时，四边形EGFH是菱形？并说明理由． （3）若四边形EGFH是正方形，请直接写出线段EF与线段BC满足的关系．（无需证明）

题型：解答题  难度：中档

答案

（1）四边形EGFH是平行四边形．理由如下： ∵F、G分别是BC、BE的中点， ∴FG∥CE且FG= 1 2 CE， ∵H是CE的中点， ∴EH= 1 2 CE， ∴FG∥EH且FG=EH， ∴四边形EGFH是平行四边形； （2）点E运动到AD的中点时，四边形EGFH是菱形．理由如下： 当四边形EGFH是菱形时，EG=EH， 又∵G、H分别是BE、CE的中点， ∴BE=CE， 根据等腰梯形的对称性，AE=DE； （3）当四边形EGFH是正方形时，EF⊥GH，且EF=GH， ∵G、H分别是BE、CE的中点， ∴GH∥BC且GH= 1 2 BC， ∴EF⊥BC且EF= 1 2 BC．

据专家权威分析，试题“如图，等腰梯形ABCD中，AD∥BC，点E是线段AD上的一个动点（点E不与..”主要考查你对  三角形中位线定理，平行四边形的判定，菱形，菱形的性质，菱形的判定，梯形，梯形的中位线，正方形，正方形的性质，正方形的判定  等考点的理解。关于这些考点的“档案”如下：

三角形中位线定理平行四边形的判定菱形，菱形的性质，菱形的判定梯形，梯形的中位线正方形，正方形的性质，正方形的判定

考点名称：三角形中位线定理

• 三角形中位线定义：
  连接三角形两边中点的线段叫做三角形的中位线。一个三角形共有三条中位线。
  三角形中位线定理：
  三角形的中位线平行于第三边，并且等于它的一半。
  
  如图已知△ABC中，D，E分别是AB，AC两边中点。
  则DE平行于BC且等于BC/2

• 三角形中位线逆定理：
  
  逆定理一：在三角形内，与三角形的两边相交，平行且等于三角形第三边一半的线段是三角形的中位线。
  如图DE//BC，DE=BC/2，则D是AB的中点，E是AC的中点。
  逆定理二：在三角形内，经过三角形一边的中点，且与另一边平行的线段，是三角形的中位线。
  如图D是AB的中点，DE//BC，则E是AC的中点，DE=BC/2

• 区分三角形的中位线和中线：
  三角形的中位线是连结三角形两边中点的线段；
  三角形的中线是连结一个顶点和它的对边中点的线段。

考点名称：平行四边形的判定

• 平行四边形的判定：
  （1）定义：两组对边分别平行的四边形是平行四边形；
  （2）定理1：两组对角分别相等的四边形是平行四边形；
  （3）定理2：两组对边分别相等的四边形是平行四边形；
  （4）定理3：对角线互相平分的四边形是平行四边形
  （5）定理4：一组对边平行且相等的四边形是平行四边形。
  平行四边形的面积：S=底×高。

考点名称：菱形，菱形的性质，菱形的判定

• 菱形的定义:
  在一个平面内，有一组邻边相等的平行四边形是菱形。

• 菱形的性质:
  ①菱形具有平行四边形的一切性质；
  ②菱形的对角线互相垂直且平分，并且每一条对角线平分一组对角；
  ③菱形的四条边都相等；
  ④菱形既是轴对称图形（两条对称轴分别是其两条对角线所在的直线），也是中心对称图形（对称中心是其重心，即两对角线的交点）；
  ⑤在有一个角是60°角的菱形中，较短的对角线等于边长，较长的对角线是较短的对角线的根号3倍。

• 菱形的判定:
  在同一平面内，
  （1）定义：有一组邻边相等的平行四边形是菱形
  （2）定理1：四边都相等的四边形是菱形
  （3）定理2：对角线互相垂直的平行四边形是菱形
  菱形是在平行四边形的前提下定义的，首先它是平行四边形，而且是特殊的平行四边形，特殊之处就是“有一组邻边相等”，因而增加了一些特殊的性质和判定方法。
  菱形的面积：S_菱形=底边长×高=两条对角线乘积的一半。

考点名称：梯形，梯形的中位线

• 梯形的定义：
  一组对边平行，另一组对边不平行的四边形叫做梯形。
  梯形中平行的两边叫做梯形的底，通常把较短的底叫做上底，较长的底叫做下底，梯形中不平行的两边叫做梯形的腰，梯形的两底的距离叫做梯形的高。
  梯形的中位线：
  连结梯形两腰的中点的线段。 

• 梯形性质：
  ①梯形的上下两底平行；
  ②梯形的中位线（两腰中点相连的线叫做中位线）平行于两底并且等于上下底和的一半。
  ③等腰梯形对角线相等。

  梯形判定：
  1.一组对边平行，另一组对边不平行的四边形是梯形。
  2.一组对边平行且不相等的四边形是梯形。
  
  梯形中位线定理：
  梯形中位线平行于两底，并且等于两底和的一半。
  梯形中位线×高=（上底+下底）×高=梯形面积
  梯形中位线到上下底的距离相等
  中位线长度=（上底+下底）