已知:△ABC中,AB=a.如图(1),若A1、B1分别是CA、CB的中点,则A1B1=a2;如图(2),若A1、A2、B1、B2分别是CA、CB的三等分点,则A1B1+A2B2=2+13a=a;如图(3),若A1、A2、A3、B1-数学
题文
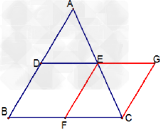
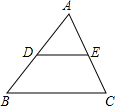
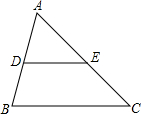
| 已知:△ABC中,AB=a. 如图(1),若A1、B1分别是CA、CB的中点,则A1B1=
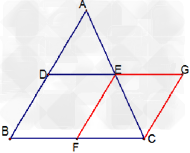
如图(2),若A1、A2、B1、B2分别是CA、CB的三等分点,则A1B1+A2B2=
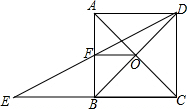
如图(3),若A1、A2、A3、B1、B2、B3分别是CA、CB的四等分点,则A1B1+A2B2+A3B3=
如图(4),若A1、A2、A3、…A9、B1、B2、B3、…B9分别是CA、CB的十等分点,则A1B1+A2B2+A3B3+…+A9B9=______.  |