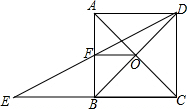
在直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=2BC=2CD,对角线AC与BD相交于点O,线段OA,OB的中点分别为点E,F.(1)求证:△FOE≌△DOC;(2)求sin∠OEF的值;(3)若直线EF与线段AD,BC分-数学
题文
在直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=2BC=2CD,对角线AC与BD相交于点O,线段 OA,OB的中点分别为点E,F. (1)求证:△FOE≌△DOC; (2)求sin∠OEF的值; (3)若直线EF与线段AD,BC分别相交于点G,H,求
|