题文

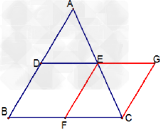
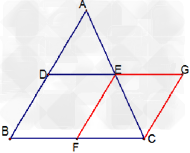
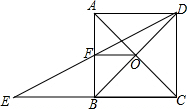
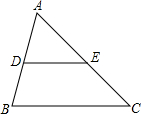
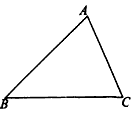
已知任意四边形ABCD，且线段AB、BC、CD、DA、AC、BD的中点分别是E、F、G、H、P、Q． （1）若四边形ABCD如图1，判断下列结论是否正确（正确的在括号里填“√”， 错误的在括号里填“×”）． 甲：顺次连接EF、FG、GH、HE一定得到平行四边形；（　　） 乙：顺次连接EQ、QG、GP、PE一定得到平行四边形．（　　） （2）请选择甲、乙中的一个，证明你对它的判断． （3）若四边形ABCD如图2，请你判断（1）中的两个结论是否成立？

题型：解答题  难度：中档

答案

（1）甲√；乙√． （2）证明：（1）中对甲的判断： 连接EF、FG、GH、HE． ∵E、F分别是AB、BC的中点， ∴EF∥AC，EF= 1 2 AC． 同理，得HG∥AC，HG= 1 2 AC， ∴EF∥HG，EF=HG， ∴四边形EFGH是平行四边形． （3）类似于（1）中的结论（甲、乙都成立）和证明．

据专家权威分析，试题“已知任意四边形ABCD，且线段AB、BC、CD、DA、AC、BD的中点分别是..”主要考查你对  三角形中位线定理，平行四边形的判定，矩形，矩形的性质，矩形的判定  等考点的理解。关于这些考点的“档案”如下：

三角形中位线定理平行四边形的判定矩形，矩形的性质，矩形的判定

考点名称：三角形中位线定理

• 三角形中位线定义：
  连接三角形两边中点的线段叫做三角形的中位线。一个三角形共有三条中位线。
  三角形中位线定理：
  三角形的中位线平行于第三边，并且等于它的一半。
  
  如图已知△ABC中，D，E分别是AB，AC两边中点。
  则DE平行于BC且等于BC/2

• 三角形中位线逆定理：
  
  逆定理一：在三角形内，与三角形的两边相交，平行且等于三角形第三边一半的线段是三角形的中位线。
  如图DE//BC，DE=BC/2，则D是AB的中点，E是AC的中点。
  逆定理二：在三角形内，经过三角形一边的中点，且与另一边平行的线段，是三角形的中位线。
  如图D是AB的中点，DE//BC，则E是AC的中点，DE=BC/2

• 区分三角形的中位线和中线：
  三角形的中位线是连结三角形两边中点的线段；
  三角形的中线是连结一个顶点和它的对边中点的线段。

考点名称：平行四边形的判定

• 平行四边形的判定：
  （1）定义：两组对边分别平行的四边形是平行四边形；
  （2）定理1：两组对角分别相等的四边形是平行四边形；
  （3）定理2：两组对边分别相等的四边形是平行四边形；
  （4）定理3：对角线互相平分的四边形是平行四边形
  （5）定理4：一组对边平行且相等的四边形是平行四边形。
  平行四边形的面积：S=底×高。

考点名称：矩形，矩形的性质，矩形的判定

• 矩形:
  是一种平面图形，矩形的四个角都是直角，同时矩形的对角线相等，而且矩形所在平面内任一点到其两对角线端点的距离的平方和相等。

• 矩形的性质：
  1．矩形的4个内角都是直角；
  2．矩形的对角线相等且互相平分；
  3．矩形所在平面内任一点到其两对角线端点的距离的平方和相等；
  4．矩形既是轴对称图形，也是中心对称图形（对称轴是任何一组对边中点的连线），它至少有两条对称轴。对称中心是对角线的交点。
  5．矩形是特殊的平行四边形，矩形具有平行四边形的所有性质
  6.顺次连接矩形各边中点得到的四边形是菱形

• 矩形的判定：
  ①定义：有一个角是直角的平行四边形是矩形
  ②定理1：有三个角是直角的四边形是矩形
  ③定理2：对角线相等的平行四边形是矩形
  ④对角线互相平分且相等的四边形是矩形
  矩形的面积：S_矩形=长×宽=ab。

• 黄金矩形:
  宽与长的比是（√5-1）/2（约为0.618）的矩形叫做黄金矩形。
  黄金矩形给我们一协调、匀称的美感。世界各国许多著名的建筑，为取得最佳的视觉效果，都采用了黄金矩形的设计。如希腊的巴特农神庙等。