一个均匀的小立方体,它的6个面上分别标有实数5.1,34,16,π2,11,8.任意掷出这个小立方体,朝上的面标有无理数的概率是()A.16B.13C.12D.23-数学
希伯索斯的发现,第一次向人们揭示了有理数系的缺陷,证明了它不能同连续的无限直线等同看待,有理数并没有布满数轴上的点,在数轴上存在着不能用有理数表示的“孔隙”。而这种“孔隙”经后人证明简直多得“不可胜数”。于是,古希腊人把有理数视为连续衔接的那种算术连续统的设想彻底地破灭了。不可公度量的发现连同芝诺悖论一同被称为数学史上的第一次数学危机,对以后2000多年数学的发展产生了深远的影响,促使人们从依靠直觉、经验而转向依靠证明,推动了公理几何学和逻辑学的发展,并且孕育了微积分思想萌芽。
不可约的本质是什么?长期以来众说纷纭,得不到正确的解释,两个不可通约的比值也一直认为是不可理喻的数。15世纪意大利著名画家达.芬奇称之为“无理的数”,17世纪德国天文学家开普勒称之为“不可名状”的数。
然而真理毕竟是淹没不了的,毕氏学派抹杀真理才是“无理”。人们为了纪念希伯索斯这位为真理而献身的可敬学者,就把不可通约的量取名“无理数”——这就是无理数的由来。
考点名称:概率的意义
- 概率的意义:
一般地,在大量重复试验中,如果事件A发生的频率 会稳定在某个常数p附近,那么这个常数p就叫做事件A的概率,记作P(A)=p,概率从某种数量上刻画一个不确定事件发生的可能性的大小。
会稳定在某个常数p附近,那么这个常数p就叫做事件A的概率,记作P(A)=p,概率从某种数量上刻画一个不确定事件发生的可能性的大小。
事件和概率的表示方法:一般地,事件用英文大写字母A,B,C,…,表示事件A的概率p,可记为P(A)=P。
事件的概率:必然事件的概率为1,不可能事件的概率为0,随机事件A的概率为0<P(A)<1。
注:(1)在n试验中,事件A发生的频率m满足0≤m≤n,所以0≤ ≤1,故0≤P(A)≤1;
≤1,故0≤P(A)≤1;
(2)P(A)=0表示事件A是不可能发生的事件,P(A)=1表示事件A是必然发生的事件;
(3)概率越大,表示事件发生的可能性越大;概率越小,表示事件发生的可能性越小;
(4)人们通常对随机事件进行大量的反复试验来研究概率,一般大量试验事件发生的频率可作为概率的估计值。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:在227,8,-3.1416,π,25,0.61161116…,39中无理数有()A.2个B.3个C.4个D.5个-数学
下一篇:在π2,3.1,-3,49,0.8080080008…,14,2,227,38,-52,36,325,中无理数的个数有______个.-数学
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |

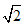

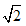
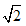
![给出四个数-1,0,0.5,,其中为无理数的是[]A.-1.B.0C.0.5D.-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/19/2019-02-24/560e6fd8b998d202f031648a254299d5.png)
