在-π3,3-127,22,0.3030030003,-227,3.14,(2)0中有理数的个数是()A.2个B.3个C.4个D.5个-数学
题文
在-
|
答案
显然-
因此它也是有理数; 所以已知的7个数中,是有理数的为:
故选D. |
据专家权威分析,试题“在-π3,3-127,22,0.3030030003,-227,3.14,(2)0中有理数的..”主要考查你对 无理数的定义,零指数幂(负指数幂和指数为1) 等考点的理解。关于这些考点的“档案”如下:
无理数的定义零指数幂(负指数幂和指数为1)
考点名称:无理数的定义
- 无理数定义:
即非有理数之实数,不能写作两整数之比。若将它写成小数形式,小数点之后的数字有无限多个,并且不会循环。 常见的无理数有大部分的平方根、π和e(其中后两者同时为超越数)等。
无理数是无限不循环小数。如圆周率π、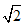 等。
等。 - 无理数性质:
无限不循环的小数就是无理数 。换句话说,就是不可以化为整数或者整数比的数
性质1 无理数加(减)无理数既可以是无理数又可以是有理数
性质2 无理数乘(除)无理数既可以是无理数又可以是有理数
性质3 无理数加(减)有理数一定是无理数
性质4 无理数乘(除)一个非0有理数一定是无理数 - 无理数与有理数的区别:
1、把有理数和无理数都写成小数形式时,有理数能写成有限小数和无限循环小数,
比如:4=4.0,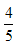 =0.8,
=0.8,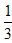 =0.33333……
=0.33333……
而无理数只能写成无限不循环小数,
比如: =1.414213562…………
=1.414213562…………
根据这一点,人们把无理数定义为无限不循环小数;
2、所有的有理数都可以写成两个整数之比,而无理数不能。根据这一点,有人建议给无理数摘掉,把有理数改叫为“比数”,把无理数改叫为“非比数”。 无理数的识别:
判断一个数是不是无理数,关键就看它能不能写出无限不循环小数,而把无理数写成无限不循环小数,不但麻烦,而且还是我们利用现有知识无法解决的难题。
初中常见的无理数有三种类型:
(1)含根号且开方开不尽的方根,但切不可认为带根号的数都是无理数;
(2)化简后含π的式子;
(3)不循环的无限小数。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:在数3.14、3、π、0.1212…、227、25、2-1中,无理数的个数有______个.-数学
下一篇:在π、227、5、0、3-1、3.1415、144、2.123122312233…中,属于无理数的个数有()个.A.2个B.3个C.4个D.5个-数学
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |


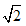
![给出四个数-1,0,0.5,,其中为无理数的是[]A.-1.B.0C.0.5D.-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/19/2019-02-24/560e6fd8b998d202f031648a254299d5.png)
