在22,π4,1.732,3-127,0.3,16,-227,30.8等数中,无理数的个数有______.-数学
无限不循环的小数就是无理数 。换句话说,就是不可以化为整数或者整数比的数
性质1 无理数加(减)无理数既可以是无理数又可以是有理数
性质2 无理数乘(除)无理数既可以是无理数又可以是有理数
性质3 无理数加(减)有理数一定是无理数
性质4 无理数乘(除)一个非0有理数一定是无理数
1、把有理数和无理数都写成小数形式时,有理数能写成有限小数和无限循环小数,
比如:4=4.0,
 =0.8,
=0.8, =0.33333……
=0.33333……而无理数只能写成无限不循环小数,
比如:
 =1.414213562…………
=1.414213562…………根据这一点,人们把无理数定义为无限不循环小数;
2、所有的有理数都可以写成两个整数之比,而无理数不能。根据这一点,有人建议给无理数摘掉,把有理数改叫为“比数”,把无理数改叫为“非比数”。
无理数的识别:
判断一个数是不是无理数,关键就看它能不能写出无限不循环小数,而把无理数写成无限不循环小数,不但麻烦,而且还是我们利用现有知识无法解决的难题。
初中常见的无理数有三种类型:
(1)含根号且开方开不尽的方根,但切不可认为带根号的数都是无理数;
(2)化简后含π的式子;
(3)不循环的无限小数。
掌握常见无理数的类型有助于识别无理数。
无理数的历史:
毕达哥拉斯(Pythagqras,约公元前885年至公元前400年间)是古希腊的大数学家。他证明许多重要的定理,包括后来以他的名字命名的毕达哥拉斯定理(勾股弦定理),即直角三角形两直角边为边长的正方形的面积之和等于以斜边为边长的正方形的面积。毕达哥拉斯将数学知识运用得纯熟之后,觉得不能只满足于用来算题解题,于是他试着从数学领域扩大到哲学,用数的观点去解释一下世界。经过一番刻苦实践,他提出“凡物皆数”的观点,数的元素就是万物的元素,世界是由数组成的,世界上的一切没有不可以用数来表示的,数本身就是世界的秩序。在他死后大约200年,他的门徒们把这种理论加以研究发展,形成了一个强大的毕达哥拉斯学派。
公元前500年,古希腊毕达哥拉斯(Pythagoras)学派的弟子希伯索斯(Hippasus)发现了一个惊人的事实,一个正方形的对角线与其一边的长度是不可公度的(若正方形的边长为1,则对角线的长不是一个有理数),这一不可公度性与毕氏学派的“万物皆数”(指有理数)的哲理大相径庭。这一发现使该学派领导人惶恐,认为这将动摇他们在学术界的统治地位,于是极力封锁该真理的流传,希伯索斯被迫流亡他乡,不幸的是,在一条海船上还是遇到毕氏门徒,于是希伯索斯被残忍地扔进了大海。
希伯索斯的发现,第一次向人们揭示了有理数系的缺陷,证明了它不能同连续的无限直线等同看待,有理数并没有布满数轴上的点,在数轴上存在着不能用有理数表示的“孔隙”。而这种“孔隙”经后人证明简直多得“不可胜数”。于是,古希腊人把有理数视为连续衔接的那种算术连续统的设想彻底地破灭了。不可公度量的发现连同芝诺悖论一同被称为数学史上的第一次数学危机,对以后2000多年数学的发展产生了深远的影响,促使人们从依靠直觉、经验而转向依靠证明,推动了公理几何学和逻辑学的发展,并且孕育了微积分思想萌芽。
不可约的本质是什么?长期以来众说纷纭,得不到正确的解释,两个不可通约的比值也一直认为是不可理喻的数。15世纪意大利著名画家达.芬奇称之为“无理的数”,17世纪德国天文学家开普勒称之为“不可名状”的数。
然而真理毕竟是淹没不了的,毕氏学派抹杀真理才是“无理”。人们为了纪念希伯索斯这位为真理而献身的可敬学者,就把不可通约的量取名“无理数”——这就是无理数的由来。
考点名称:立方根
- 定义:
一般地,如果一个数x的立方等于a,那么这个x叫做a的立方根。
如果一个数x的立方等于a,即x的三次方等于a(x3=a),即3个x连续相乘等于a,那么这个数x就叫做a的立方根,也叫做三次方根。
数a的立方根记作 ,读作“三次根号a”。
,读作“三次根号a”。
读作:“三次根号a”其中,a叫做被开方数,3叫做根指数。(a等于所有数,包括0)如果被开方数还有指数,那么这个指数(必须是三能约去的)还可以和三次根号约去。 开立方:求一个数a的立方根的运算叫做开立方,其中a叫做被开方数。
立方根性质:
①正数的立方根是正数;负数的立方根是负数;0的立方根是0。
②一般地,如果一个数X的立方等于 a,那么这个数X就叫做a的立方根(也叫做三次方根)。
也就是说,如果x3=a,那么x叫做a的立方根。
如2是8的立方根,-3分之2是-27分之8的立方根,0是0的立方根。
③立方和开立方运算,互为逆运算。
④互为相反数的两个数的立方根也是互为相反数。
⑤负数不能开平方,但能开立方。
⑥任何数(正数、负数、或零)的立方根如果存在的话,必定只有一个。
⑦当两个数相等时,这两个数的平方根相等,反之亦然。- 平方根和立方根的关系:
区别:
⑴根指数不同:平方根的根指数为2,且可以省略不写;立方根的根指数为3,且不能省略不写。
⑵ 被开方的取值范围不同:平方根中被开方数必需为非负数;立方根中被开方数可以为任何数。
⑶ 结果不同:平方根的结果除0之外,有两个互为相反的结果;立方根的结果只有一个。
联系:
二者都是与乘方运算互为逆运算
在部分科学计算器上面需要按SHIFT键+x3才可以打出来根号。 笔算开立方的方法:
方法一
1.将被开立方数的整数部分从个位起向左每三位分为一组;
2.根据最左边一组,求得立方根的最高位数;
3.用第一组数减去立方根最高位数的立方,在其右边写上第二组数;
4.用求得的最高位数的平方的300倍试除上述余数,得出试商;并把求得的最高位数的平方的300倍与试商的积、求得的最高位数的30倍与试商的平方的积和试商的立方写在竖式左边,观察其和是否大于余数,若大于,就减小试商再试,若不大于,试商就是立方根的第二位数;
5.用同样方法继续进行下去。
方法二
第1、2步同上。
第三步,商完后,落下余数和后面紧跟着的三位,如果后面没有就把余数后面添上三个0;
第四步,将要试商的数代入式子“已商数×要试商数×(10×已商数+要试商数)×30+要商数的立方”,最接近但不超过第三步得到的数者,即为这一位要商的数。
然后重复第3、4步,直到除尽。
考点名称:算术平方根
- 概念:
若一个正数x的平方等于a,即x2=a,则这个正数x为a的算术平方根。
规定:0的算术平方根是0。
表示:a的算术平方根记为 ,读作“根号a”。
,读作“根号a”。
注:只有非负数有算术平方根,而且只有一个算术平方根。 - 平方根和算术平方根的区别与联系:
区别:
(1)定义不同:如果一个数的平方等于a,则这个数叫做a的平方根;非负数a的非负平方根叫做a的算术平方根。
(2)个数不同:一个正数有两个平方根,它们互为相反数;而一个正数的算术平方根只有一个。
(3)表示方法不同:正数a的平方根表示为± ,正数a的算术平方根表示为
,正数a的算术平方根表示为 。
。
(4)取值范围不同:正数的算术平方根一定是正数;正数的平方根一正一负,两数互为相反数。
联系:
(1)具有包含关系:平方根包含算术平方根,算术平方根是平方根的一种,是正的平方根。
(2)存在条件相同:只有非负数才有平方根和算术平方根。
(3)0的平方根,算术平方根均为0。开平方:求一个数的平方根的运算,叫做开平方。
注:
(1)平方和开平方的关系是互为逆运算;
(2)乘方是求根的途径,开平方是一种运算,是求平方根的过程;
(3)开方的方式是根号形式。 - 电脑根号的打法:
比较通用:
左手按住换档键(Alt键)不放,接着依次按41420然后松开左手,根号√ ̄就出来了。
运用Word的域命令在Word中根号:
首先按住Ctrl+F9,出现{}后,在{}内输入EQ空格\r(开方次数,根号内的表达式),最后按住Shift+F9,就会生成你所要求的根式
1.平方根
一个正数的平方根有两个,它们互为相反数。比如 9 的平方根是3,-3。而5的平方根是√5,-√5。规定,零的平方根是0。负数没有平方根。
2.算术平方根是指一个正数的正的平方根。比如 9 的算术平方根是±3。而5的算术平方根是±√5。规定,零的算术平方根是0。
算术平方根是定义在平方根基础上,因此负数没有算术平方根。
3.实数a的算术平方根记作√ ̄a,其中a≥0,根据以上定义有√ ̄a≥0。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |

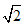

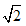
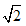
![给出四个数-1,0,0.5,,其中为无理数的是[]A.-1.B.0C.0.5D.-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/19/2019-02-24/560e6fd8b998d202f031648a254299d5.png)
