下列说法中正确的是:A.有理数与数轴上的点一一对应B.无限小数是无理数C.-32读作-3的平方D.5的平方根是±5-数学
交换律:a+b=b+a , ab=ba
结合律:(a+b)+c=a+(b+c)
分配律:a(b+c)=ab+ac
2.实数的相反数:
实数的相反数的意义和有理数的相反数的意义相同。
实数只有符号不同的两个数,它们的和为零,我们就说其中一个是另一个的相反数。
实数a的相反数是-a,a和-a在数轴上到原点0的距离相等。
3.实数的绝对值:
实数的绝对值的意义和有理数的绝对值的意义相同。一个正实数的绝对值等于它本身;
一个负实数的绝对值等于它的相反数,0的绝对值是0,实数a的绝对值是 :|a|
①a为正数时,|a|=a(不变)
②a为0时, |a|=0
③a为负数时,|a|= a(为a的相反数)
(任何数的绝对值都大于或等于0,因为距离没有负的。)
4实数的倒数:
实数的倒数与有理数的倒数一样,如果a表示一个非零的实数,那么实数a的倒数是:1/a (a≠0)
实数的分类:
(1)按定义分类:
正整数
整数 { 零
负整数
有理数{ }有限小数或无限循环小数
真分数
分数{
实数{ 负分数
正无理数
无理数{ }无限不循环小数
负无理数
(2)按性质分类:
正整数
正有理数{
正实数{ 正分数
正无理数
实数{ 零 负整数
负有理数{
负实数{ 负分数
负无理数
考点名称:平方根
- 平方根定义:
如果一个数的平方等于a,则这个数叫做a的平方根,如果x2=a,那么x叫做a的平方根,这里a是x的平方,它是一个非负数,即a≥0。
表示:一个正数有两个平方根,用 表示平方根中正的那个,用-
表示平方根中正的那个,用- 表示负的平方根。
表示负的平方根。 性质:
①一个正数如果有平方根,那么必定有两个,它们互为相反数。
显然,如果我们知道了这两个平方根的一个,那么就可以及时的根据相反数的概念得到它的另一个平方根。②如果一个正数x的平方等于a,即x的平方等于a,那么这个正数x叫做a的算术平方根。a
的算术平方根记为,读作“根号a”,a叫做被开方数。③规定:0的平方根是0。
④负数在实数范围内不能开平方,只有在复数范围内,才可以开平方根。
例如:-1的平方根为±1,-9的平方根为±3。
⑤平方根包含了算术平方根,算术平方根是平方根中的一种。
平方根和算术平方根都只有非负数才有。
被开方数是乘方运算里的幂。
求平方根可通过逆运算平方来求。
开平方:求一个非负数a的平方根的运算叫做开平方,其中a叫做被开方数。
若x的平方等于a,那么x就叫做a的平方根,即正负根号a=正负x- 1 至 20 的平方根:
利用长式除法可以求平方根。长式除法需要进行加法,减法,乘法,除法等四则运算。一般计算机软件的运算精度小于20位数字,如要计算平方根到100位,四则运算的精度需100位以上。 利用高精度长式除法可以计算出 1 至 20 的 平方根如下:

=1 
≈1.414213562373095048801688724209698078569671875376948073176679737990732478462 
≈1.732050807568877293527446341505872366942805253810380628055806979451933016909 
=2 
≈2.236067977499789696409173668731276235440618359611525724270897245410520925638 
≈2.449489742783178098197284074705891391965947480656670128432692567250960377457 
≈2.645751311064590590501615753639260425710259183082450180368334459201068823230 
≈2.828427124746190097603377448419396157139343750753896146353359475981464956924 
=3 
≈3.162277660168379331998893544432718533719555139325216826857504852792594438639 
≈3.316624790355399849114932736670686683927088545589353597058682146116484642609 - 最新内容
- 相关内容
- 网友推荐
- 图文推荐
- 在-3,-,,-,0.323232…,,0这几(2019-02-21)
- 在给出的一组数0.3,,3.14,,,-(2019-02-21)
- 若无理数a满足1<a<4,请写出一个你(2019-02-21)
- 在两个连续整数a和b之间,且a<<b,(2019-02-21)
- 在实数:π、-、、、3.14、0.01515(2019-02-21)
- 在下列各数中,无理数是[]A.-2.1B(2019-02-21)
- 在下列实数中,无理数是[]A.B.π(2019-02-21)
- 试举一列,说明“两个无理数的差仍(2019-02-21)
- 有下列说法:①任何无理数都是无限(2019-02-21)
无相关信息- 在给出的下列数3.14、π、3、0.101(2019-02-21)
- 在下列各数中是无理数的有()-0.3(2019-02-21)
- 下列各数:-732,0,1.41,327,π(2019-02-21)
- 在13、π、3、0.1010010001…(相邻(2019-02-21)
- 给出四个数-1,0,0.5,,其中为无(2019-02-21)
- 下列实数中,无理数是[]A.﹣B.π(2019-02-21)
- 下列实数π2,sin30°,0.1414,39(2019-02-21)
- 在等中,是无理数的是().-八年级(2019-02-21)
- 在-7.5,15,4,38,-π,??0.15,(2019-02-21)
- 下列各数中,是无理数的是[]A.B.-1(2019-02-21)
上一篇:有六个数0.1385,0.010010001,-30.008,π,-227,2,其中无理数的个数是()A.4B.3C.2D.1-数学 下一篇:在实数-23,0,3,-3.14,0.101001000…(每两个1之间依次多一个零),4,3-8,无理数有()个.A.2B.3C.4D.5-数学零零教育社区:论坛热帖子[家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) [教师分享] 给远方姐姐的一封信 (2018-11-07) [教师分享] 伸缩门 (2018-11-07) [教师分享] 回家乡 (2018-11-07) [教师分享] 是风味也是人间 (2018-11-07) [教师分享] 一句格言的启示 (2018-11-07) [教师分享] 无规矩不成方圆 (2018-11-07) [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) [教师分享] 贪玩的小狗 (2018-11-07) [教师分享] 未命名文章 (2018-11-07)

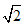

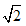
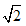
![给出四个数-1,0,0.5,,其中为无理数的是[]A.-1.B.0C.0.5D.-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/19/2019-02-24/560e6fd8b998d202f031648a254299d5.png)
