下列说法:(1)4是一个无理数;(2)8的立方根是±2;(3)函数y=1x-1的自变量x的取值范围是x>1;(4)平分弦的直径垂直于弦;(5)方程x2-2x-99=0可通过配方变形为(x-1)2=100;(6)两条-数学
区别:
⑴根指数不同:平方根的根指数为2,且可以省略不写;立方根的根指数为3,且不能省略不写。
⑵ 被开方的取值范围不同:平方根中被开方数必需为非负数;立方根中被开方数可以为任何数。
⑶ 结果不同:平方根的结果除0之外,有两个互为相反的结果;立方根的结果只有一个。
联系:
二者都是与乘方运算互为逆运算
在部分科学计算器上面需要按SHIFT键+x3才可以打出来根号。
笔算开立方的方法:
方法一
1.将被开立方数的整数部分从个位起向左每三位分为一组;
2.根据最左边一组,求得立方根的最高位数;
3.用第一组数减去立方根最高位数的立方,在其右边写上第二组数;
4.用求得的最高位数的平方的300倍试除上述余数,得出试商;并把求得的最高位数的平方的300倍与试商的积、求得的最高位数的30倍与试商的平方的积和试商的立方写在竖式左边,观察其和是否大于余数,若大于,就减小试商再试,若不大于,试商就是立方根的第二位数;
5.用同样方法继续进行下去。
方法二
第1、2步同上。
第三步,商完后,落下余数和后面紧跟着的三位,如果后面没有就把余数后面添上三个0;
第四步,将要试商的数代入式子“已商数×要试商数×(10×已商数+要试商数)×30+要商数的立方”,最接近但不超过第三步得到的数者,即为这一位要商的数。
然后重复第3、4步,直到除尽。
考点名称:一元二次方程的解法
- 一元二次方程的解:
能够使方程左右两边相等的未知数的值叫做方程的解。
解一元二次方程方程:
求一元二次方程解的过程叫做解一元二次方程方程。 韦达定理:
一元二次方程根与系数的关系(以下两个公式很重要,经常在考试中运用到)
一般式:ax2+bx+c=0的两个根x1和x2关系:
x1+x2= -b/a
x1·x2=c/a- 一元二次方程的解法:
1、直接开平方法
利用平方根的定义直接开平方求一元二次方程的解的方法叫做直接开平方法。
直接开平方法适用于解形如 的一元二次方程,根据平方根的定义可知,x+a 是b的平方根,当
的一元二次方程,根据平方根的定义可知,x+a 是b的平方根,当 时,
时, ;当b<0时,方程没有实数根。
;当b<0时,方程没有实数根。
用直接开平方法求一元二次方程的根,一定要正确运用平方根的性质,即正数的平方根有两个,它们互为相反数,零的平方根是零,负数没有平方根。
2、配方法
配方法是一种重要的数学方法,它不仅在解一元二次方程上有所应用,而且在数学的其他领域也有着广泛的应用。
配方法的理论根据是完全平方公式 ,把公式中的a看做未知数x,并用x代替,则有
,把公式中的a看做未知数x,并用x代替,则有  。
。
3、公式法
公式法是用求根公式解一元二次方程的解的方法,它是解一元二次方程的一般方法。
一元二次方程 的求根公式:
的求根公式:
求根公式是专门用来解一元二次方程的,故首先要求a≠0;有因为开平方运算时,被开方数必须是非负数,所以第二个条件是b2-4ac≥0。即求根公式使用的前提条件是a≠0且b2-4ac≥0。
4、因式分解法
因式分解法就是利用因式分解的手段,求出方程的解的方法,这种方法简单易行,是解一元二次方程最常用的方法。
考点名称:对顶角,同位角,内错角,同旁内角
对顶角:
一个角的两边分别是另一个角的反向延升线,这两个角是对顶角两条直线相交后所得的只有一个公共顶点且两个角的两边互为反向延长线,这样的两个角叫做互为对顶角。
两条直线相交,构成两对对顶角。互为对顶角的两个角相等(对顶角的性质)。
对顶角是针对具有特殊位置的两个角的名称;
对顶角相等反映的是两个角之间的大小关系。同位角:两个都在截线的同旁,又分别处在被截的两条直线同侧的位置的角叫做同位角。
内错角:两个角分别在截线的两侧,且在两条被截直线之间,具有这样位置关系的一对角叫做内错角。
同旁内角: 两个角都在截线的同一侧,且在两条被截线之间,具有这样位置关系的一对角互为同旁内角。
- 各种角的关系图示:

直线AB,CD与EF相交(或者说两条直线AB,CD被第三条直线EF所截),构成八个角。
如图中,∠1与∠3,∠2与∠4是对顶角。
其中∠1与∠5这两个角分别在AB,CD的上方,并且在EF的同侧,像这样位置相同的一对角叫做同位角;
∠3与∠5这两个角都在AB,CD之间,并且在EF的异侧,像这样位置的两个角叫做内错角;
∠3与∠6在直线AB,CD之间,并侧在EF的同侧,像这样位置的两个角叫做同旁内角。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |

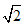

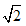
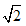
![给出四个数-1,0,0.5,,其中为无理数的是[]A.-1.B.0C.0.5D.-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/19/2019-02-24/560e6fd8b998d202f031648a254299d5.png)
