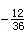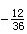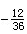下列叙述正确的是()①数轴上的点与实数一一对应;②若a<b,则a<b;③若五个数的积为负数,则其中正因数有2个或4个;④近似数3.70是由a四舍五入得到的,则a的范围为3.695≤a<3.-数学
(1)同号两数相乘,取正号,并把绝对值相乘;
(2)异号两数相乘,取负号,并把绝对值相乘;
(3)任何数与0相乘都得0。
几个不等于0的数相乘,积的符号由负因数的个数决定,当负因数有奇数个时,积为负;当负因数有偶数个时,积为正。
有理数乘法的运算律:
(1)交换律:ab=ba;
(2)结合律:(ab)c=a(bc);
(3)分配律:a(b+c)=ab+ac。
1.几个不为0的数相乘,积的符号由负因数的个数决定,当负因数的个数是奇数时,积的符号为负;相反,当负因数的个数是偶数时,积的符号为正。
2.几个数相乘,只要有一个数为0,积就是0。
乘法法则的推广:
1.几个不等于零的数相乘,积的符号由负因数的个数决定,当负因数有奇数个时,积为负;当负因数有偶数个时,积为正;
2.几个数相乘,有一个因数为零,积就为零;
3.几个不等于零的数相乘,首先确定积的符号,然后把绝对值相乘。
有理数乘法的注意:
1.乘法是指求几个相同加数的和的简便算法,引入负数后,乘法的意义没有改变;
2.有理数乘法与有理数加法的运算步骤一样:确定符号、确定绝对值;
3.掌握乘法法则的关键是会确定积的符号:“两数相乘,同号得正,异号得负”,切勿与有理数加法的符号法则混淆。
考点名称:近似数和有效数字
- 近似数:
一个数与准确数相近(比准确数略多或者略少些),这一个数称之为近似数。
如:我国的人口无法计算准确数目,但是可以说出一个近似数。
比如说我国人口有13亿,13亿就是一个近似数。
有效数字:
是指从该数字左边第一个非0的数字到该数字末尾的数字个数(有点绕口)。例如:
3一共有1个有效数字,0.0003有一个有效数字,0.1500有4个有效数字,1.9×103有两个有效数字(不要被103迷惑,只需要看1.9的有效数字就可以了,10n看作是一个单位)。
精确度:
近似数与准确数的接近程度,可以用精确度表示。
(1)一个近似数四舍五入到哪一位,就说这个近似数精确到哪一位;
(2)规定有效数字的个数,也是对近似数精确程度的一种要求。 - 有效数字注意:
①近似数的精确度有两种形式:精确到哪一位;保留几个有效数字;
②对于绝对值较大的数取近似值时,结果一般用科学计数法来表示,如:8 90 000(保留三个有效数字)的近似值,得8 903 000≈8.90×106。
③对带有计数单位的近似数,如2.3万,他有两个有效数字:2、3,而不是五个有效数字。 - 有效数字的舍入规则:
1、当保留n位有效数字,若后面的数字小于第n位单位数字的0.5就舍掉。
2、当保留n位有效数字,若后面的数字大于第n位单位数字的0.5 ,则第位数字进1。
3、当保留n位有效数字,若后面的数字恰为第n位单位数字的0.5 ,则第n位数字若为偶数时就舍掉后面的数字,若第n位数字为奇数加1。
如将下组数据保留三位
45.77=45.8 43.03=43.0
38.25=38.2 47.15=47.2
考点名称:实数的比较大小
- 实数的比较大小法则:
正实数都大于0,负实数都小于0;
正实数大于一切负实数,两个负实数绝对值大的反而小;
在数轴上,右边的数要比左边的大。
- 实数比较大小的具体方法:
(1)求差法:
设a,b为任意两个实数,先求出a与b的差,再根据
“当a-b<0时,a<b;当a-b=0时,a=b;当a-b>0时,a>b”来比较a与b的大小。
(2)求商法:
设a,b(b≠0)为任意两个正实数,先求出a与b的商,再根据
“当 <1时,a<b;当
<1时,a<b;当 =1时,a=b;当
=1时,a=b;当 >1时,a>b”来比较a与b的大小;
>1时,a>b”来比较a与b的大小;
当a,b(b≠0)为任意两个负实数时,再根据
“当 <1时,a>b;当
<1时,a>b;当 =1时,a=b;当
=1时,a=b;当 >1时,a<b” 来比较a与b的大小。
>1时,a<b” 来比较a与b的大小。
(3)倒数法:
设a,b(a≠0,b≠0)为任意两个正实数,先分别求出a与b的倒数,再根据
“当 <
< 时,a>b;当
时,a>b;当 >
> 时,a<b。”来比较a与b的大小。
时,a<b。”来比较a与b的大小。
(4)平方法:
比较含有无理数的式子的大小时,先将要比较的两个数分别平方,再根据
“在a>0,b>0时,可由a2>b2 得到a>b”比较大小。
也就是说,两个正数比较大小时,如果一个数的平方比另一个数的平方大,则这个数大于另一个数。
还有估算法、近似值法等。
两个实数的大小比较,形式有多种多样,只要我们在实际操作时,有选择性地灵活运用上述方法,一定能方便快捷地取得令人满意的结果。
(5)数轴比较法:
实数与数轴上的点一一对应。
利用这条性质,将实数的大小关系转化为点的位置关系。
设数轴的正方向指向右方,则数轴上右边的点所表示的数比左边的点所表示的数要大。
如图,点A表示数a,点B表示数b。因为点A在点B的右边,所以数a大于数b,即a>b.
考点名称:直线,线段,射线
- 基本概念:
直线:一根拉得很紧的线,就给我们以直线的形象,直线是直的,并且是向两方无限延伸的。一条直线可以用一个小写字母表示。
线段:直线上两个点和它们之间的部分叫做线段,这两个点叫做线段的端点。一条线段可用它的端点的两个大写字母来表示。
射线:直线上一点和它一旁的部分叫做射线。这个点叫做射线的端点。一条射线可以用端点和射线上另一点来表示。
注意:
①线和射线无长度,线段有长度。
②直线无端点,射线有一个端点,线段有两个端点。 直线、射线、线段的基本性质:
图形 表示法 端点 延长线 能否度量 基本性质 直线 没有端点的一条线 一条线,
不要端点无 可以向两边无限延长 否 两端都没有端点,可以无限延长,不可测量的线 射线 只有一个端点的一条线 一条线,
只有一边有端点一个 可以向一边无限延长 否 一端有端点,可以向一边无限延长,不可测量的线 线段 两边都有端点的一条线 一条线,两边都有端点 两个 不能延长 能 两端都有端点,不能延长,可测量的线 - 直线、射线、线段区别:
直线没有端点,2边可无限延长;
射线有1端有端点,另一端可无限延长;
线段,有2个端点,而2个端点间的距离就是这条线段的长度。
直线除了“直”这个特点外,还有一个很重要的特点,那就是它可以向两个方向无限延伸,永远没有尽头,所以,直线是不可能度量的。因此,在画直线时,要画出没有端点的直线,表示可以无限延伸;
射线只有一个端点,可以向一个方向无限延伸,也永远没有尽头。所以,射线也是不可能度量的。直线上任意的一点可以把这条直线分成两条方向相反的射线,因此,射线是直线的一部分。虽然射线是直线的一部分,但由于它们都是不能度量的,所以,它们之间没有长短可以比较;
线段有两个端点,它有一定的长度,可以度量。线段也是直线的一部分。 - 各种图形表示方法:
直线:一个小写字母或两个大写字母,但前面必须加“直线”两字,如:直线l,直线m;直线AB,直线CD。
例: 直线l;直线AB。
直线l;直线AB。
射线:一个小写字母或端点的大写字母。和射线上的一个大写字母,前面必须加“射线”两字。如:射线a;射线OA。
例: 射线AB。
射线AB。
线段:用表示端点的大写字母表示,如线段AB;用一个小写字母表示,如线段a。
例: 线段AB;线段a 。
线段AB;线段a 。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
无相关信息
上一篇:与数轴上的点一一对应的数是()A.整数B.有理数和无理数C.有理数D.无理数-数学
下一篇:下列四种说法正确的有()个.(1)无限小数一定是无理数(2)数轴上的每一个点都表示实数(3)负数没有立方根(4)数轴上左边的数总比右边的数小A.1个B.2个C.3个D.4个-数学
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |