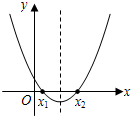
已知:二次函数y=x2-4x-a,下列说法错误的是()A.当x<1时,y随x的增大而减小B.若图象与x轴有交点,则a≤4C.当a=3时,不等式x2-4x+a<0的解集是1<x<3D.若将图象向上平移1个单位,-数学
为什么人们对13这个数如此回避呢?说法很多。
有一种说法是:我们现在通用的十进制是以数10作为基础的,可是在古罗马则是采用十二进制算法的。到后来,把12作为“一打”的计算方法为欧洲许多国家所采用。因此,12成了家喻户晓的进位制的殿军。这样一来,人们对12以后的数就产生一种莫明其妙的感觉,以致认为13这个数是个不祥的数,是个危险的数,所以后来人们就忌讳使用这样的数。
另一个理论是来自柏林一位医生威廉姆?福利斯。他认为人类有史以来的一切活动和一切对象皆可以用一个简单的公式“23x+28y”来表示,
一年有365天,而365=23×11+28×4;
法国大革命开始于1789年,而1789=23×23+28×45;
人类细胞核中有46对染色体,而46=23×2+28×0;
《圣经》中动物的数目是666,而666=23×18+28×9。
然而,“不幸”的事终于发生在13这个数上:
13=23×3+28×(-2)
这个式子中出现了负数,它是“不幸”的。当然,这些都是一些无稽之谈,是没有科学根据的。
"1名数学家=10个师"的由来:
第二次世界大战中,美国曾经宣称:一名优秀的数学家的作用超过10个师的兵力。你可知这句话的由来吗?
1943年以前,在大西洋上英美运输船队常常受到德国潜艇的袭击,当时,英美两国限于实力,无力增派更多的护航舰,一时间,德军的"潜艇战"搞得盟军焦头烂额。
为此,有位美国海军将领专门去请教了几位数学家,数学家们运用概率论分析后发现,舰队与敌潜艇相遇是一个随机事件,按数学角度来看这一问题,它有一定的规律。一定数量的船(如100艘)编队规模越小,编次就越多(如每次20艘,就要有5个编次);编次越多,与敌人相遇的概率就越大。比如5位同学放学都回自己家里,老师要找一位同学的话,随便去哪家都行,但若这5位同学都在其中某一家的话,老师要找几家才能找到,一次找到的可能性只有20%。
美国海军接受了数学家的建议,命令船队在指定海域集合,再集体通过危险海域,然后各自驶向预定港口。结果奇迹出现了:盟军舰队遭袭被击沉的概率由原来的25%降低为1%,大大减少了损失,保证了物资的及时供应。
考点名称:二次函数的定义
- 定义:
一般地,如果 (a,b,c是常数,a≠0),那么y叫做x 的二次函数。
(a,b,c是常数,a≠0),那么y叫做x 的二次函数。
①所谓二次函数就是说自变量最高次数是2;
②二次函数 (a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时,
(a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时, 变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。
变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。
③二次函数 (a≠0)与一元二次方程
(a≠0)与一元二次方程 (a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
(a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。 - 二次函数的解析式有三种形式:
(1)一般式: (a,b,c是常数,a≠0);
(a,b,c是常数,a≠0);
(2)顶点式: (a,h,k是常数,a≠0)
(a,h,k是常数,a≠0)
(3)当抛物线 与x轴有交点时,即对应二次好方程
与x轴有交点时,即对应二次好方程 有实根x1和x2存在时,根据二次三项式的分解因式
有实根x1和x2存在时,根据二次三项式的分解因式 ,二次函数
,二次函数 可转化为两根式
可转化为两根式 。如果没有交点,则不能这样表示。
。如果没有交点,则不能这样表示。
二次函数的一般形式的结构特征:
①函数的关系式是整式;
②自变量的最高次数是2;
③二次项系数不等于零。 - 二次函数的判定:
二次函数的一般形式中等号右边是关于自变量x的二次三项式;
当b=0,c=0时,y=ax2是特殊的二次函数;
判断一个函数是不是二次函数,在关系式是整式的前提下,如果把关系式化简整理(去括号、合并同类项)后,能写成 (a≠0)的形式,那么这个函数就是二次函数,否则就不是。
(a≠0)的形式,那么这个函数就是二次函数,否则就不是。
考点名称:二次函数的图像
- 二次函数的图像
是一条关于 对称的曲线,这条曲线叫抛物线。
对称的曲线,这条曲线叫抛物线。
抛物线的主要特征:
①有开口方向,a表示开口方向:a>0时,抛物线开口向上;a<0时,抛物线开口向下;
②有对称轴;
③有顶点;
④c 表示抛物线与y轴的交点坐标:(0,c)。 二次函数图像性质:
轴对称:
二次函数图像是轴对称图形。对称轴为直线x=-b/2a
对称轴与二次函数图像唯一的交点为二次函数图像的顶点P。
特别地,当b=0时,二次函数图像的对称轴是y轴(即直线x=0)。
a,b同号,对称轴在y轴左侧
b=0,对称轴是y轴
a,b异号,对称轴在y轴右侧
顶点:
二次函数图像有一个顶点P,坐标为P ( h,k )
当h=0时,P在y轴上;当k=0时,P在x轴上。即可表示为顶点式y=a(x-h)^2+k。
h=-b/2a, k=(4ac-b^2)/4a。
开口:
二次项系数a决定二次函数图像的开口方向和大小。
当a>0时,二次函数图像向上开口;当a<0时,抛物线向下开口。
|a|越大,则二次函数图像的开口越小。- 决定对称轴位置的因素:
一次项系数b和二次项系数a共同决定对称轴的位置。
当a>0,与b同号时(即ab>0),对称轴在y轴左; 因为对称轴在左边则对称轴小于0,也就是- b/2a<0,所以 b/2a要大于0,所以a、b要同号
当a>0,与b异号时(即ab<0),对称轴在y轴右。因为对称轴在右边则对称轴要大于0,也就是- b/2a>0, 所以b/2a要小于0,所以a、b要异号
可简单记忆为左同右异,即当a与b同号时(即ab>0),对称轴在y轴左;当a与b异号时(即ab<0 ),对称轴在y轴右。
事实上,b有其自身的几何意义:二次函数图像与y轴的交点处的该二次函数图像切线的函数解析式(一次函数)的斜率k的值。可通过对二次函数求导得到。
决定与y轴交点的因素:
常数项c决定二次函数图像与y轴交点。
二次函数图像与y轴交于(0,C)
注意:顶点坐标为(h,k), 与y轴交于(0,C)。
与x轴交点个数:
a<0;k>0或a>0;k<0时,二次函数图像与x轴有2个交点。
k=0时,二次函数图像与x轴只有1个交点。
a<0;k<0或a>0,k>0时,二次函数图像与X轴无交点。
当a>0时,函数在x=h处取得最小值ymin=k,在x<h范围内是减函数,在x>h范围内是增函数(即y随x的变大而变小),二次函数图像的开口向上,函数的值域是y>k
当a<0时,函数在x=h处取得最大值ymax=k,在x<h范围内是增函数,在x>h范围内是减函数(即y随x的变大而变大),二次函数图像的开口向下,函数的值域是y<k
当h=0时,抛物线的对称轴是y轴,这时,函数是偶函数。
考点名称:二次函数与一元二次方程
- 二次函数与一元二次方程的关系:
函数y=ax2+bx+c(a≠0),当y=0时,得到一元二次方程ax2+bx+c=0(a≠0)。
那么一元二次方程的解就是二次函数图像与x轴焦点的横坐标,因此,二次函数图像与x轴的交点情况决定一元二次方程根的情况。
1、从形式上看:
二次函数:y=ax2+bx+c (a≠0)
一元二次方程:ax2+bx+c=0 (a≠0)
2、从内容上看:
二次函数表示的是一对(x,y)之间的关系,它有无数对解;一元二次方程表示的是未知数x的值,最多只有2个值
3、相互关系:
二次函数与x轴交点的横坐标就是相应的一元二次方程的根。
如:y=x2-4x+3与x轴的交点是(1,0)、(3,0),则一元二次方程x2-4x+3=0的根是x=1或x=3 二次函数交点与二次方程根的关系:
抛物线y=ax2+bx+c与x轴的交点个数可由一元二次方程ax2+bx+c=0的根的情况说明:
1、若△>0,则一元二次方程ax2+bx+c=0有两个不等的实数根,则抛物线y=ax2+bx+c与x轴有两个交点---相交;
2、若△=0,则一元二次方程ax2+bx+c=0有两个相等的实数根,则抛物线y=ax2+bx+c与x轴有唯一公共点---相切(顶点);
3、若△<0,则一元二次方程ax2+bx+c=0没有实数根,则抛物线y=ax2+bx+c与x轴没有公共点--相离。
若抛物线y=ax2+bx+c与轴的两个交点坐标分别是A(x1,0),B(x2,0),则x1+x2=- ,x1x2=
,x1x2= 。
。点拨:
①解一元二次方程实质上就是求当二次函数值为0时的自变量x的取值,反映在图像上就是求抛物线与x轴交点的横坐标。
②若一元二次方程ax2+bx+c=0(a≠0)的两根为x1,x2(x1<x2),则抛物线y=ax2+bx+c与x轴的交点为(x1,0),(x2,0),对称轴为x=x1+x2/2。
③若a>0,当x<x1,或x>x2时,y>0;当x1<x<x2时,y<0。
若a< 0,当x1
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |