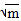在报道溢油的多少和影响以及准备清除工作时,数据是非常必要的.为了说明数据是如何重要,读一读这则关于一次有名的溢油事件的“被删去”的文章.在______、______,一艘大型油轮-数学
题文
| 在报道溢油的多少和影响以及准备清除工作时,数据是非常必要的.为了说明数据是如何重要,读一读这则关于一次有名的溢油事件的“被删去”的文章. 在______、______,一艘大型油轮Exxon Valdez从阿拉斯加水道离开,载着______原油,为了避免撞上冰山,这艘轮船走了一条离开正常行船线路大约______的航线,不幸的是,在离港不到______,船碰上了水下的暗礁,暗礁的岩石将船体撞了一个______裂缝,______原油溢到威廉玛海峡的表面,几个星期后,尽管花了很多的努力控制和清理石油,这次Exxon Valdez溢油事件已成为一个被全球关注的环境灾难,溢出的油不断地扩展形成一个油膜,覆盖了______水面,杀死了______只水獭和______只鸟,清理工作用了______只船和工人,工人们与______寒冷的水和气温作斗争,清理工作花费______,包括______单独用于营救野生生物的费用. (1)从以下所列的数据中,将恰当的数据填在相应的空白处,解释说明你的每一选择. 2000km2;46 000 000L;4 100 000美元; 2000~3000;18 000cm;1600m; 4℃;90 000~300 000;240 000 000 L; 20亿美元;1989年3月24日;下午9:00;成千上万;3h. (2)理解大数目的一种方法是找到尺寸相同的熟悉的事物、例如:美国旧金山和纽约合在一起的面积约为2000 km2,Exxon Valdez的油膜大约覆盖这两个城市.理解大数目的另一个方法是考证复制熟悉的事物.例如:美国公立学校,每个学生的平均花费为4500美元,营救Exxon Valdez事件中的野生生物所花费的金钱和9000多名学生的花费差不多. 在A~G中,给出了关于Exxon Valdez灾难中的事实,假如你是一位被分派撰写这一报道的报社记者,用你自己的观点将所给的提示写出一个说明,在某种程度上让你的读者容易理解每一个事实. a、Exxon Valdez溢出原油46 000 000 L. 提示:一个奥林匹克标准游泳池可容纳大约2 270 000 L的水,多少个游泳池可装满46 000 000 L的油? b、油船偏离航道大约1600m、 提示:你所在的地区,什么地方相距大约1600m? c、在清理溢油期间,水和空气的温度大约为4℃、 提示:你所在的地区,水和空气什么时候达到这个温度,你还游泳吗? d、在离港不到3 h,油船触礁、 提示:你熟悉的什么事情持续3h? e、溢油杀死了90 000~300 000只海鸟、 提示:查阅资料,找出人口数量大约为300 000这个数目的城市、 f、整个清理工作花费2 000 000 000美元、 提示:在美国,付给工人每年平均工资大约为25 000美元,清理工作所花费的付给多少工人的年度工资? g、油膜最后覆盖了海洋表面2000 km2、 提示:计算你们教室地面的面积,然后计算出需要多少这样的教室的地面才能覆盖2000 km2. |
答案
| (1)A为1989年3月24日,B为下午9:00;显然A、B处填的是时间,一般年、月、日在前,具体时间在后; C为240000000L;载着多少原油,问的是体积,那么应选240000000L; D为1600m;大约多少的航线,讲的是距离,因此选1600m; E为3h;离港不到多少时,船撞上了暗礁,显然问的是时间,所以选3h; F为18000cm,船的裂缝长显然不可能是1600m,那么只有选18000cm; G为46000000L,G、C问的都是原油的体积,但是根据题意,显然G<C,因此G选46000000L; H为2000km2,覆盖了多少水面,问的是面积的大小,所以选2000km2; I为2000--3000;J为90000--3000000;I、J说的都是被杀死的动物的数量,显然水獭的数量要比水鸟少的多; K为成千上万;由于海水被原油和动物尸体等污染的面积较大,因此需要的船只和人数的数量很大,故选成千上万; L为4℃;显然L问的是水温,因此选4℃; M为20亿美元;N为4100000美元;M、N问的是钱数,显然M中包括N,故M选20亿美元,N选4100000美元. (2)a、大约需20、3个游泳池; b、学校到体育馆 c、应城; d、上午上班的时间; e、扬州城市人口也为30万; f、80000个工人; g、20 000 000个教室的地面. |
据专家权威分析,试题“在报道溢油的多少和影响以及准备清除工作时,数据是非常必要的.为..”主要考查你对 数学常识 等考点的理解。关于这些考点的“档案”如下:
数学常识
考点名称:数学常识
- 数学:
在生活中,我们经常会用到一些数学上的知识,数学和我们人类的生活是息息相关的。
了解数学的由来和发展,比方说阿拉伯数字的由来了,加减乘除符号的由来,著名的命题“万物皆数”是由毕达哥拉斯提出的等等这些关于数学上的基本常识性问题。 学习数学的意义:
有这样一个传说,一次,数学家欧基里德教一个学生学习某个定理。结束后这个年轻人问欧基里德,他学了能得到什么好处。欧基里德叫过一个奴隶,对他说:“给他3个奥波尔,他说他学了东西要得到好处。”在数学还非常哲学化的古希腊,探究世界的本原、万物之道,而要得到什么“好处”,受到鄙视是可以理解的。这就像另一个故事:在巴黎的一个酒吧里,一个姑娘问她的情人迟到的原因,那年轻人说他在赶做一道数学题,姑娘摇着脑袋,不解地问:“我真不明白,你花那么多时间搞数学,数学到底有什么用啊?”那年轻人长久地看着她,然后说:“宝贝儿,那么爱情,到底有什么用啊?”
由经验构成的分散的知识,显然没有成体系的知识可信,我们历来都对知识的体系更有信任感。例如牛顿的力学体系,可以精确地计算物体的运动,即使推测1亿年的日食也几乎丝毫不差;达尔文以物种进化和自然选择为核心的进化论,把整个生物世界统括为一个有序的、有机的系统,使得我们知道不同物种之间的关系。
但是,即使是经典的知识体系,也不足以始终承载我们的全部信任,因为新的经验、新的研究会调整、更新旧的知识体系,新理论会替代旧理论。爱因斯坦相对论的出现,使得牛顿的力学体系成为一种更广泛理论中的特例;基因学说的发展和化石证据的积累,使得达尔文进化论中渐变的思想受到挑战,这样的事例充满了整个科学发展的历史,让我们不时用怀疑的眼光打量一下那些仿佛无懈可击的知识体系,对它们心存警惕。
不过,在人们追求确定性、可靠性的时候,还有一块安宁的绿洲,那就是数学。数学是我们最可信赖的科学,什么东西一经数学的证明,便板上钉钉,确凿无疑。另外,新的数学理论开拓新的领域,可以包容但不会否定已有的理论。数学是惟一一门新理论不推翻旧理论的科学,这也是数学值得信赖的明证。
终极的确定
数学追求什么?我们称古希腊的贤哲泰勒斯是古代数学第一人,是因为他不像埃及或巴比伦人那样,对任意一个规则物体求数值解,他的雄心是揭示一个系列的真理。比如圆,他的答案不是关于一个特殊圆,而是任意圆,他对全世界所有的圆感兴趣,他创造的理想的圆可以断言:任何经过圆心的直线都将圆分割为两等分,他找到的真理揭示了圆的性质。
数学要求普遍的确定性。
数学要划清结果和证明的界限。
世界再变幻不定,我们也总要有所凭信,有所依托,把这种凭信的根据推到极致,我们能体会到数学的力量。数学之大用也在于此。
我们的先人很早就开始用数学来解决具体的工程问题,在这方面,各古文明都有上佳的表现,但是古希腊人对数学的理解更值得我们敬佩。首先是毕达哥拉斯学派,他们把数看作是构成世界的要素,世上万物的关系都可以用数来解析,这绝不是我们现代“数字地球”之类的概念可以比拟的,那是一种世界观,万物最终可以归结为数,由数学说明的东西可以成为神圣的信仰,我想,持这样想法的人,一定对自然常存敬畏,不会专横自欺的。
其次,古希腊人把数学用于辩论,他们要求数学提供关于政治、法律、哲学论点的论据,要求绝对可靠的证据,要求“不可驳斥性”;他们也不满足于(例如埃及、巴比伦前辈那样的)经验性的证据,而是进一步要求证明,要求普遍的确定性。多么可爱、严正的要求!有这样要求的人,必定明达事理,光明磊落。
为了保证思想可靠,古希腊的思想家制定了思想的规则,在人类历史上,思想第一次成为思想的对象,这些规则我们称之为逻辑。比如不可同时承认正命题和反命题,换句话说,一个论点和它的反论点不能同时为真,即矛盾律;比如一正论点与反论点不可同时为假,即排中律。所有这些努力,都特别体现着人类对确定、可靠的知识的追求,一部数学史,就是人类不断扩大确知领域的历史最古老的的数学趣题:
在七间房子里,每间都养着七只猫;在这七只猫中,不论哪只,都能捕到七只老鼠;而这七只老鼠,每只都要吃掉七个麦穗;如果每个麦穗都能剥下七颗麦粒,请问:房子、猫、老鼠、麦穗、麦粒,都加在一起总共该有多少数?
答案:总数是19607。
房子有7间,猫有72=49只,鼠有73=343只,麦穗有74=2401个,麦粒有75=16807合。全部加起来是7+72+73+74+75=19607。
可以说这是世界上最古老的数学趣题了。大约在公元前1800年,埃及的一个僧侣名叫阿默士,他在纸草书上写有如下字样:
家 猫 鼠 麦 量器
7 49 343 2401 16807
但他没有说明是什么意思。
两千多年后,意大利的裴波那契在《算盘书》(1202年)中写了这样一个问题:“7个老妇同赴罗马,每人有7匹骡,每匹骡驮7个袋,每个袋盛7个面包,每个面包带有7把小刀,每把小刀放在7个鞘之中,问各有多少?”受到这个问题的启发,德国著名的数学史家M·康托尔认明阿默士的题意和这个题所问是相同的。
这类问题,在19世纪初又以歌谣体出现在算术书中:
我赴圣地爱弗西,
途遇妇女数有七,
一人七袋手中提,
一袋七猫数整齐,
一猫七子紧相依,
妇与布袋猫与子,
几何同时赴圣地?数学符号的起源:
数学除了记数以外,还需要一套数学符号来表示数和数、数和形的相互关系。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |