(本小题满分10分)问题再现现实生活中,镶嵌图案在地面、墙面乃至于服装面料设计中随处可见.在八年级课题学习“平面图形的镶嵌”中,对于单种多边形的镶嵌,主要研究了三角形、-数学
题文
| (本小题满分10分) 问题再现 现实生活中,镶嵌图案在地面、墙面乃至于服装面料设计中随处可见.在八年级课题学习“平面图形的镶嵌”中,对于单种多边形的镶嵌,主要研究了三角形、四边形、正六边形的镶嵌问题.今天我们把正多边形的镶嵌作为研究问题的切入点,提出其中几个问题,共同来探究. 我们知道,可以单独用正三角形、正方形或正六边形镶嵌平面.如图,用正方形镶嵌平面,可以发现在一个顶点O周围围绕着4个正方形的内角.  试想:如果用正六边形镶嵌平面,在一个顶点周围应该围绕 个正六边形内角. 问题提出 如果我们要同时用两种不同的正多边形镶嵌平面,可能设计出几种不同的组合方案? 问题解决 猜想1:是否可以同时用正方形、正八边形两种正多边形组合进行平面镶嵌? 分析:我们可以将此问题转化为数学问题来解决.从平面图形的镶嵌中可以发现,解决问题的关键在于分析能同时用于完整镶嵌平面的两种正多边形的内角特点.具体地说,就是在镶嵌平面时,一个顶点周围围绕的各个正多边形的内角恰好拼成一个周角. 验证1:在镶嵌平面时,设围绕某一点有x个正方形和y个正八边形的内角可以拼成一个周角.根据题意,可得方程:  ,整理得: ,整理得: , ,我们可以找到惟一一组适合方程的正整数解为  . . 结论1:镶嵌平面时,在一个顶点周围围绕着1个正方形和2个正八边形的内角可以拼成一个周角,所以同时用正方形和正八边形两种正多边形组合可以进行平面镶嵌. 猜想2:是否可以同时用正三角形和正六边形两种正多边形组合进行平面镶嵌?若能,请按照上述方法进行验证,并写出所有可能的方案;若不能,请说明理由. 上面,我们探究了同时用两种不同的正多边形组合镶嵌平面的部分情况,仅仅得到了一部分组合方案,相信同学们用同样的方法,一定会找到其它可能的组合方案. 问题拓广 请你仿照上面的研究方式,探索出一个同时用三种不同的正多边形组合进行平面镶嵌的方案,并写出验证过程. |
答案
| 略 |
解:3个; ·········· 1分 验证2:在镶嵌平面时,设围绕某一点有a个正三角形和b个正六边形的内角可以拼成一个周角.根据题意,可得方程:  . . 整理得:  , , 可以找到两组适合方程的正整数解为  和 和 .······ 3分 .······ 3分结论2:镶嵌平面时,在一个顶点周围围绕着2个正三角形和2个正六边形的内角或者围绕着4个正三角形和1个正六边形的内角可以拼成一个周角,所以同时用正三角形和正六边形两种正多边形组合可以进行平面镶嵌. 5分 猜想3:是否可以同时用正三角形、正方形和正六边形三种正多边形组合进行平面镶嵌?· 6分 验证3:在镶嵌平面时,设围绕某一点有m个正三角形、n个正方形和c个正六边形的内角可以拼成一个周角. 根据题意,可得方程:  , ,整理得:  , ,可以找到惟一一组适合方程的正整数解为  . ········ 8分 . ········ 8分结论3:镶嵌平面时,在一个顶点周围围绕着1个正三角形、2个正方形和1个正六边形的内角可以拼成一个周角,所以同时用正三角形、正方形和正六边形三种正多边形组合可以进行平面镶嵌. (说明:本题答案不惟一,符合要求即可.) 10分 |
据专家权威分析,试题“(本小题满分10分)问题再现现实生活中,镶嵌图案在地面、墙面乃至..”主要考查你对 计算器的使用,截一个几何体 ,七巧板 等考点的理解。关于这些考点的“档案”如下:
计算器的使用截一个几何体 七巧板
考点名称:计算器的使用
- 计算器:
这一小小的程序机器实际上是从计算机中割裂出来的衍生品,但因其方便快捷的操作模式,已经被广泛应用于工程、学习、商业等日常生活中,极大的方便了人们对于数字的整合运算。 - 科学计算器中的按键含义:
Backspace :删除当前输入的最后一位数。
CE :清除当前显示的数,不影响已经输入的数。
C :清除当前的计算,开始新的计算。
MC :清除存储器中的数据。
MR:调用存储器中的数据。
MS:存储当前显示的数据。
M+:将显示的数据加到存储器中,与已存入的数据相加。
Mod求模(即整数相除求余数)
And按位与, Or按位或, Xor按位异或
Lsh左移, Not按位取反, Int取整数部分
pi圆周率, Exp允许输入用科学计数法表示的数字
dms度分秒切换
cos余弦, sin正弦, tan正切,
log常用对数, n!阶乘, ln自然对数,
F-E科学计数法开关 普通计算器的使用方法:
M+:是计算结果并加上已经储存的数;中断数字输入.
M-:从存储器内容中减去当前显示值;中断数字输入.
MRC:第一次按下此键将调用存储器内容,第二次按下时清除存储器内容.
MR:调用存储器内容.
MC:清除存储器内容.
GT:按下GT键,传送GT存储寄存器内容到显示寄存器;按AC或C键消除GT显示标志.
例如:文具店卖出笔3支,每支10元;胶带2卷,每卷9.5元;橡皮3个,每个1.2元,如果用计算器,如何计算他们的总和?
可以先计算器上算出10*3=30后,按M+存起来(存储器默认存着0),再按9.5*2=,算出结果后按M+,再按1.2*3=得到结果后再按M+这样存储器里就是这几个结果的加和了,再按MR就出来结果了。
考点名称:截一个几何体
- 截面的定义:
用一个平面去截一个几何体,截出的面叫截面。由前面的知识知道,“面与面相交得到线”,用平面去截几何体,所得到的截面就是这个平面与几何体每个面相交所围成的图形。 - 用平面截一个几何体所得截面的形状:
截面的形状多为圆和多边形,也可能是不规则图形,一般与下面两点有关:
(1)几何体的形状;
(2)切截的方向和角度。
一般的,截面与几何体的几个面相交,就得到几条交线,截面与平面相交就得到几边形;
截面与曲面相交,得到曲线,截面是圆或不规则图形。 - 几种常见几何体的截面:
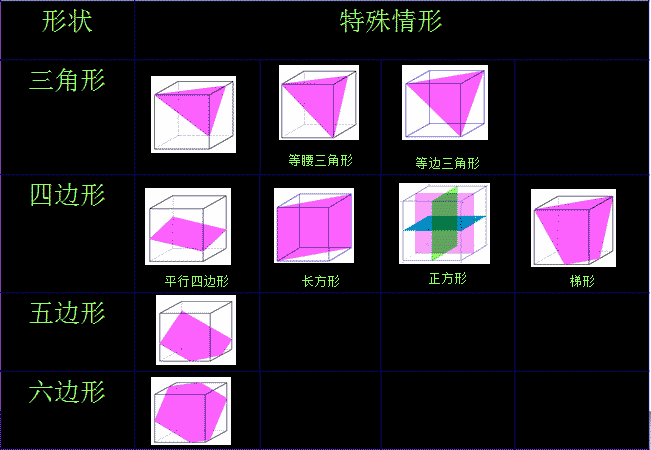
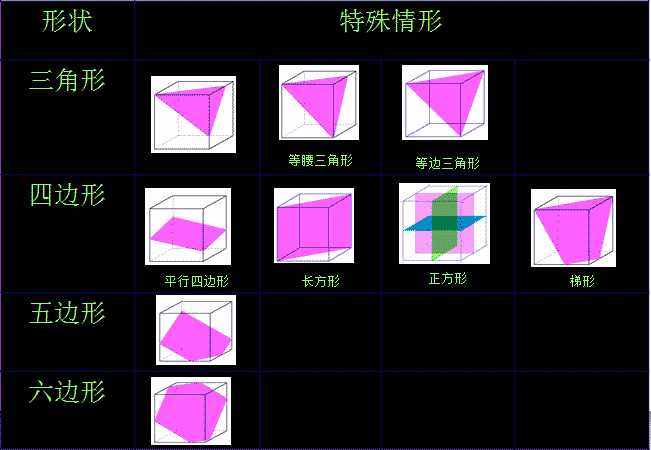
①正方体的截面有:
三角形,等腰三角形,等边三角形;
正方形,长方形,平行四边形,菱形,梯形
五边形,六边形
②圆柱的截面:
圆,椭圆,长方形,不规则图形;
③圆锥的截面:
圆,椭圆,等腰三角形,不规则图形 - 正方体截面图情况:

考点名称:七巧板
- 七巧板:
是一种智力游戏,顾名思义,是由七块板组成的。而这七这块板可拼成许多图形(1600种以上),例如:三角形、平行四边形、不规则多边形、玩家也可以把它拼成各种人物、形象、动物、桥、房、塔等等,亦可是一些中、英文字母。 游戏规则:
七巧板是一种拼图游戏,它是用七块板,以各种不同的拼凑法来拼搭千变万化的形象图案。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |