为支持抗震救灾,我市A、B两地分别向灾区捐赠物资100吨和180吨。需全部运往重灾区C、D两县,根据灾区的情况,这批赈灾物资运往C县的数量比运往D县的数量的2倍少80吨。(1)求这-七年级数学
题文
| 为支持抗震救灾,我市A、B两地分别向灾区捐赠物资100吨和180吨。需全部运往重灾区C、D两县,根据灾区的情况,这批赈灾物资运往C县的数量比运往D县的数量的2倍少80吨。 (1)求这批赈灾物资运往C、D两县的数量各是多少吨? (2)设A地运往C县的赈灾物资为x吨(x为整数),若要B地运往C县的赈灾物资数量大于A地运往D县的赈灾物资数量的2倍,且要求B地运往D县的赈灾物资数量不超过63吨,则A、B两地的赈灾物资运往C、D两县的方案有几种? |
答案
| ⑴ 运往C,D两县的数量各是160吨,120吨。 ⑵方案共有三种,分别为: ①A运往C县41吨,B运往C 县119吨 ;A运往D县59吨,B运往D 县61吨 ②A运往C县42吨,B运往C 县118吨 ;A运往D县58吨,B运往D 县62吨 ③A运往C县43吨,B运往C 县117吨 ;A运往D县57吨,B运往D 县63吨 |
试题分析:(1)设这批赈灾物资运往D县的数量为x;根据题意得 x+2x-80=100+180 解得x=120 所以这批赈灾物资运往C县的数量为  (2)由(1)知这批赈灾物资运往C、D两县的数量各是160吨,120吨 设A地运往C县的赈灾物资为x吨(x为整数);若要B地运往C县的赈灾物资数量大于A地运往D县的赈灾物资数量的2倍,为支持抗震救灾,我市A、B两地分别向灾区捐赠物资100吨和180吨,则2(100-x);根据题意x+2(100-x)<160,解得x>40;A地运往C县的赈灾物资为100-x吨; 因为要求B地运往D县的赈灾物资数量不超过63吨,即小于等于63,所以100-x+63  120,解得 120,解得 ,综合上述情况,A地运往C县的赈灾物资为 ,综合上述情况,A地运往C县的赈灾物资为 ,又因为x为整数,所以x只能取41,42,43,方案共有三种;分别如下 ,又因为x为整数,所以x只能取41,42,43,方案共有三种;分别如下A运往C县41吨,B运往C 县119吨 ;A运往D县59吨,B运往D 县61吨 ②A运往C县42吨,B运往C 县118吨 ;A运往D县58吨,B运往D 县62吨 ③A运往C县43吨,B运往C 县117吨 ;A运往D县57吨,B运往D 县63吨 点评:本题考查方程,不等式,解答本题需要考生通过审题列出方程并解答方程,以及熟悉一元一次不等式的解法,正确的解答出不等式组的解来,本题看起比较复杂,其实难度不算大 |
据专家权威分析,试题“为支持抗震救灾,我市A、B两地分别向灾区捐赠物资100吨和180吨。..”主要考查你对 计算器的使用,截一个几何体 ,七巧板 等考点的理解。关于这些考点的“档案”如下:
计算器的使用截一个几何体 七巧板
考点名称:计算器的使用
- 计算器:
这一小小的程序机器实际上是从计算机中割裂出来的衍生品,但因其方便快捷的操作模式,已经被广泛应用于工程、学习、商业等日常生活中,极大的方便了人们对于数字的整合运算。 - 科学计算器中的按键含义:
Backspace :删除当前输入的最后一位数。
CE :清除当前显示的数,不影响已经输入的数。
C :清除当前的计算,开始新的计算。
MC :清除存储器中的数据。
MR:调用存储器中的数据。
MS:存储当前显示的数据。
M+:将显示的数据加到存储器中,与已存入的数据相加。
Mod求模(即整数相除求余数)
And按位与, Or按位或, Xor按位异或
Lsh左移, Not按位取反, Int取整数部分
pi圆周率, Exp允许输入用科学计数法表示的数字
dms度分秒切换
cos余弦, sin正弦, tan正切,
log常用对数, n!阶乘, ln自然对数,
F-E科学计数法开关 普通计算器的使用方法:
M+:是计算结果并加上已经储存的数;中断数字输入.
M-:从存储器内容中减去当前显示值;中断数字输入.
MRC:第一次按下此键将调用存储器内容,第二次按下时清除存储器内容.
MR:调用存储器内容.
MC:清除存储器内容.
GT:按下GT键,传送GT存储寄存器内容到显示寄存器;按AC或C键消除GT显示标志.
例如:文具店卖出笔3支,每支10元;胶带2卷,每卷9.5元;橡皮3个,每个1.2元,如果用计算器,如何计算他们的总和?
可以先计算器上算出10*3=30后,按M+存起来(存储器默认存着0),再按9.5*2=,算出结果后按M+,再按1.2*3=得到结果后再按M+这样存储器里就是这几个结果的加和了,再按MR就出来结果了。
考点名称:截一个几何体
- 截面的定义:
用一个平面去截一个几何体,截出的面叫截面。由前面的知识知道,“面与面相交得到线”,用平面去截几何体,所得到的截面就是这个平面与几何体每个面相交所围成的图形。 - 用平面截一个几何体所得截面的形状:
截面的形状多为圆和多边形,也可能是不规则图形,一般与下面两点有关:
(1)几何体的形状;
(2)切截的方向和角度。
一般的,截面与几何体的几个面相交,就得到几条交线,截面与平面相交就得到几边形;
截面与曲面相交,得到曲线,截面是圆或不规则图形。 - 几种常见几何体的截面:
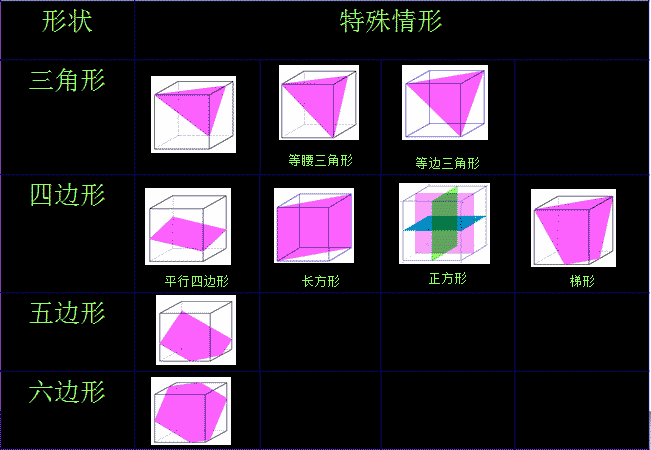
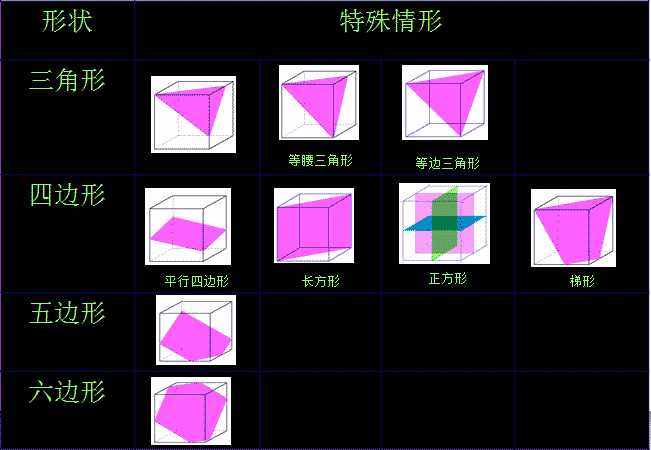
①正方体的截面有:
三角形,等腰三角形,等边三角形;
正方形,长方形,平行四边形,菱形,梯形
五边形,六边形
②圆柱的截面:
圆,椭圆,长方形,不规则图形;
③圆锥的截面:
圆,椭圆,等腰三角形,不规则图形 - 正方体截面图情况:

考点名称:七巧板
- 七巧板:
是一种智力游戏,顾名思义,是由七块板组成的。而这七这块板可拼成许多图形(1600种以上),例如:三角形、平行四边形、不规则多边形、玩家也可以把它拼成各种人物、形象、动物、桥、房、塔等等,亦可是一些中、英文字母。 游戏规则:
七巧板是一种拼图游戏,它是用七块板,以各种不同的拼凑法来拼搭千变万化的形象图案。
将一块正方形的板按图所示分割成七块,就成了七巧板。用这七块板可以拼搭成几何图形,如三角形、平行四边形、不规则的多角形等;也可以拼成各种具体的人物形象,或者动物,如猫、狗、猪、马等;或者是桥、房子、宝塔,或者是一些中、英文字符号以及数字。
具体玩法:
通常,用七巧板拼摆出的图形应当由全部的七块板组成,且板与板之间要有连接,如点的连接、线的连接或点与线的连接;可以一个人玩,也可以几个人同时玩。
七巧板的玩法有4种:
①依图成形,即从已知的图形来排出答案;
②见影排形,从已知的图形找出一种或一种以上的排法;
③自创图形,可以自己创造新的玩法、排法;
④数学研究,利用七巧板来求解或证明数学问题。
七巧板按不同的方法拼摆、组合可以拼排成各种各样的几何图形和形象,如桥梁、船只、房屋、手枪或是跑步、跌倒、玩耍、跳舞、站立的人物以及戏水的鱼、猫、狗等。
操作七巧板是一种发散思维活动,有利于培养人们的观察力、注意力、想像力和创造力,因此,不仅具有娱乐的价值,还具有一定的教育价值,被人们运用到了教学当中。
由于七巧板可以持续不断地反复组合,已引起哲学、心理学、美学等多领域的研究者的兴趣,还被作为制作商业广告和印章的辅助手段。- 七巧板的好处与用处简直是多不胜数,例如:形状概念、视觉分辨、认智技巧、视觉记忆、手眼协调、鼓励开放、扩散思考、创作机会。
无论在现代或古代,七巧板都是用以启发幼儿智力的良好伙伴。能够把幼儿对实物与形态之间的桥梁连接起来,培养幼儿的观察力、想像力、形状分析及创意逻辑上都有巨大的发展空间。
制作七巧板:
制作七巧板是一件十分简单的事。材料也只是普通文具:一支笔、一把尺、一把剪刀和一块纸板(纸张),几只彩笔。
1.首先,在纸上画一个正方形,把它分为十六个小方格。
2.再从左上角到右下角画一条线。
3.在上面的中间连一条线到右面的中间。
4.再在左下角到右上角画一条线,碰到第二条线就可以停了。
5.从刚才的那条线的尾端开始一条线,画左上与右下的对角线的四分之三,另外,在左上右下这条对对角线的四分之一处画一条线,与上边的中间相连。
6.最后,把它们涂上不同的颜色并沿着黑线条剪开,你就有一副全新的七巧板。 七巧板的历史发展:
“七巧板”是我国古代劳动人民的发明,其历史至少可以追溯到公元前一世纪,到了明代基本定型。明、清两代在民间广泛流传,清陆以湉《冷庐杂识》卷一中写道“近又有七巧图,其式五,其数七,其变化之式多至千余。体物肖形,随手变幻,盖游戏之具,足以排闷破寂,故世俗皆喜为之。”
“七巧图”不知何时传到国外,受到他们的欢迎与重视,李约瑟说它是“东方最古老的消遣品”之一,至今英国剑桥大学的图书馆里还珍藏着一部《七巧新谱》。美国作家埃德加·爱伦坡特竟用象牙精制了一副七巧板。法国拿破仑在流放生活中也曾用七巧板作为消遣游戏。谁能想象到七巧板居然会跟拿破仑·波拿巴、亚当、杜雷、爱伦坡特以及卡洛尔等人发生关系?实际上他们全都是七巧板的狂热爱好者。
玩过七巧板吗?那简简单单的七块板,竟能拼出千变万化的图形。谁能想到呢,这种玩具是由一种古代家具演变来的。
宋朝有个叫黄伯思的人,对几何图形很有研究,他热情好客,发明了一种用6张小桌子组成的“宴几”——请客吃饭的小桌子。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |