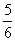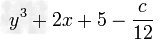下列说法错误的是()A.单项式-πab23的系数是-13π,次数是3B.反比例函数的图象经过(-2,1)则这个函数图象一定在第二、四象限C.随意抛掷一枚骰子,出现6点的概率为16D.圆锥侧面-数学
题文
下列说法错误的是( )
|
答案
| A |
据专家权威分析,试题“下列说法错误的是()A.单项式-πab23的系数是-13π,次数是3B.反比例..”主要考查你对 单项式,反比例函数的图像,概率的意义,圆锥的计算 等考点的理解。关于这些考点的“档案”如下:
单项式反比例函数的图像概率的意义圆锥的计算
考点名称:单项式
- 单项式:
表示数或字母的积的式子叫做单项式。
单项式中的数字因数叫做这个单项式的系数,一个单项式中,所有字母的指数的和叫做这个单项式的次数。任何一个非零数的零次方等于1。 单项式性质:
1.分母含有字母的式子不属于单项式。因为单项式属于整式,而分母含有未知数的式子是分式。例如:1/x不是单项式。
分母中不含字母(单项式是整式,而不是分式)
a,-5,X,2XY,都是单项式,而0.5m+n,不是单项式。
2.单独的一个数字或字母也是单项式。例如:1和x2y也是单项式。
3.任意一个字母和数字的积的形式的代数式(除法中有:除以一个数等于乘这个数的倒数)。
4.如果一个单项式,只含有字母因数,如果是正数的单项式系数为1,如果是负数的单项式系数为-1。
5.如果一个单项式,只含有数字因数,那么它的次数为0。
6.0也是数字,也属于单项式。
7.有分数也属于单项式。
单项式的次数与系数:
1.单项式是字母与数的乘积。
单项式的次数:一个单项式中,所有字母的指数的和叫做这个单项式的次数。
单项式的系数:单项式中的数字因数。
单项式是几次,就叫做几次单项式。
如:2xy的系数是2;-5zy 的系数是-5
字母t的指数是1,100t是一次单项式;
在单项式vt中,字母v与t的指数的和是2,vt是二次单项式。
如:xy ,3,a z,ab,b ...... 都是单项式。
单项式书写规则:
1.单项式表示数与字母相乘时,通常把数写在前面;
2.乘号可以省略为点或不写;
3.除法的式子可以写成分数式;
4.带分数与字母相乘,带分数要化为假分数
5.π是常数,因此也可以作为系数。(“π”是特指的数,不是字母,读pài。)
6.当一个单项式的系数是1或-1时,“1”通常省略不写,如[(-1)ab ]写成[ -ab ]等。
7.在单项式中字母不可以做分母,分子可以。字母不能在分母中(因为这样为分式,不为单项式)
8.单独的数“0”的系数是零,次数也是零。
9.常数的系数是它本身,次数为零。单项式的运算法则:
加减法则
单项式加减即合并同类项,也就是合并前各同类项系数的和,字母不变。
例如:3a+4a=7a,9a-2a=7a等。
同时还要运用到去括号法则和添括号法则。
乘法法则
单项式相乘,把它们的系数、相同字母分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式
例如:3a·4a=12a^2
除法法则
同底数幂相除,底数不变,指数相减。
例如:9a10÷3a5=3a5
考点名称:反比例函数的图像
- 反比例函数的图象:
反比例函数的图像是双曲线,它有两个分支,这两个分支分别位于第一、三象限,或第二、四象限,它们关于原点对称。由于反比例函数中自变量x≠0,函数y≠0,所以,它的图像与x轴、y轴都没有交点,即双曲线的两个分支无限接近坐标轴,但永远达不到坐标轴。
反比例函数的图像属于以原点为对称中心的中心对称的双曲线,反比例函数图像中每一象限的每一支曲线会无限接近X轴Y轴但不会与坐标轴相交(y≠0)。 - 反比例函数图象的画法:
(1)列表:
(2)描点:在平面直角坐标系中标出点。
(3)连线:用平滑的曲线连接点。
当双曲线在一三象限,K>0,在每个象限内,Y随X的增大而减小。
当双曲线在二四象限,K<0,在每个象限内,Y随X的增大而增大。
常见画法当两个数相等时那么曲线呈弯月型。 - k的意义及应用:
过反比例函数 (k≠0),图像上一点P(x,y),作两坐标轴的垂线,两垂足、原点、P点组成一个矩形,矩形的面积
(k≠0),图像上一点P(x,y),作两坐标轴的垂线,两垂足、原点、P点组成一个矩形,矩形的面积 。过反比例函数过一点,作垂线,三角形的面积为
。过反比例函数过一点,作垂线,三角形的面积为 。
。
研究函数问题要透视函数的本质特征。反比例函数中,比例系数k有一个很重要的几何意义,那就是:过反比例函数图象上任一点P作x轴、y轴的垂线PM、PN,垂足为M、N则矩形PMON的面积
所以,对双曲线上任意一点作x轴、y轴的垂线,它们与x轴、y轴所围成的矩形面积为常数。从而有k的绝对值。在解有关反比例函数的问题时,若能灵活运用反比例函数中k的几何意义,会给解题带来很多方便。
推论内容:一次函数y=x+b或y=-x+b若与反比例函数 存在两个交点,若设2点的横坐标分别为x1,x2,那么这两个交点与原点连线和两点之间的连线所构成的三角形面积为
存在两个交点,若设2点的横坐标分别为x1,x2,那么这两个交点与原点连线和两点之间的连线所构成的三角形面积为
- 不同象限分比例函数图像:

常见画法:
考点名称:概率的意义
- 概率的意义:
一般地,在大量重复试验中,如果事件A发生的频率 会稳定在某个常数p附近,那么这个常数p就叫做事件A的概率,记作P(A)=p,概率从某种数量上刻画一个不确定事件发生的可能性的大小。
会稳定在某个常数p附近,那么这个常数p就叫做事件A的概率,记作P(A)=p,概率从某种数量上刻画一个不确定事件发生的可能性的大小。
事件和概率的表示方法:一般地,事件用英文大写字母A,B,C,…,表示事件A的概率p,可记为P(A)=P。
事件的概率:必然事件的概率为1,不可能事件的概率为0,随机事件A的概率为0<P(A)<1。
注:(1)在n试验中,事件A发生的频率m满足0≤m≤n,所以0≤ ≤1,故0≤P(A)≤1;
≤1,故0≤P(A)≤1;
(2)P(A)=0表示事件A是不可能发生的事件,P(A)=1表示事件A是必然发生的事件;
(3)概率越大,表示事件发生的可能性越大;概率越小,表示事件发生的可能性越小;
(4)人们通常对随机事件进行大量的反复试验来研究概率,一般大量试验事件发生的频率可作为概率的估计值。
考点名称:圆锥的计算
圆锥:
以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的面所围成的东西叫做圆锥体。该直角边叫圆锥的轴。
圆锥的组成构件:
①圆锥的高:圆锥的顶点到圆锥的底面圆心之间的距离叫做圆锥的高;
②圆锥的母线:圆锥的侧面展开形成的扇形的半径、底面圆周上点到顶点的距离。
③圆锥的侧面积:将圆锥的侧面沿母线展开,是一个扇形,这个扇形的弧长等于圆锥底面的周长,而扇形的半径等于圆锥的母线的长。
圆锥的侧面积就是弧长为圆锥底面的周长×母线/2;没展开时是一个曲面。
④圆锥有一个底面、一个侧面、一个顶点、一条高、无数条母线,且底面展开图为一圆形侧面展开图是扇形。
⑤圆锥侧面展开是一个扇形,已知扇形面积为二分之一rl。所以圆锥侧面积为二分之一母线长×弧长(即底面周长)。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |

 的系数是-
的系数是- ,次数是3
,次数是3


![在代数式,2∏x2y,,﹣5,a,0中,单项式的个数是[]A.1B.2C.3D.4-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/28/2019-02-28/963e7a83688d5c687d40363c599d1c91.png)