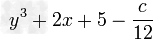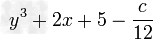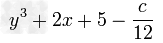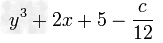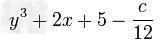题文

如果x3-6x2+14x-9=（x-1）（x2+mx+n），求； （1）m、n的值；  （2）m+n的平方根；   （3）7m+2mn的立方根．

题型：解答题  难度：中档

答案

（1）由题意知 x3-6x2+14x-9=（x-1）（x2+mx+n）=x3+mx2+nx-x2-mx-n， =x3+（m-1）x2-（m-n）x-n， m-1=-6， 解得：m=-5， -（m-n）=14， ∵m=-5， ∴n=9， （2）m+n的平方根为：± m+n =± -5+9 =± 4 =2； （3）7m+2mn的立方根为： 3 7m+2mn = 3 7×(-5)+2×(-5)×9 = 3 -125 =-5．

据专家权威分析，试题“如果x3-6x2+14x-9=（x-1）（x2+mx+n），求；（1）m、n的值；（2）m+n的平..”主要考查你对  多项式 ，平方根，立方根  等考点的理解。关于这些考点的“档案”如下：

多项式 平方根立方根

考点名称：多项式

• 多项式：
  几个单项式的和叫做多项式。多项式中，每个单项式叫做多项式的项，不含字母的项叫做常数项，这些单项式中的最高次数，就是这个多项式的次数。多项式和单项式统称为整式。

• 多项式性质：
  1、多项式的次数：多项式中次数最高的项的次数；
  2、多项式的排列：把一个多项式按某一个字母的指数从大到小的顺序排列起来叫做把这个多项式按这个字母的降幂排列；
  3、把一个多项式按某一个字母的指数从小到大的顺序排列起来叫做把这个多项式按这个字母的升幂排列。
  4、多项式项数：若多项式以最少的单项式之和呈现，则每一个单项式都被称为此多项式的项，而项的数目称为项数。
  例如：多项式  的项数是四，故称为四项式。当中的都是此多项式的项。
  5、多项式的“元”：多项式中的变量种类称为元，各种变量以各字母表达(注:通常是x、y、z)，一个多项式有n种变量就称为n元多项式。
  例如：中有x、y二元，是二元多项式。因有四项，可称二元四项式。

• 多项式的运算：
  1.加法与乘法：
           多项式的加法：是指多项式中同类项的系数相加，字母保持不变(即合并同类项)。多项式的乘法,是指把一个多项式中的每个单项式与另一个多项式中的每个单项式相乘之后合并同类项。
  例如：
  也可以用矩阵乘法来进行：
  
  
  2.多项式除法:
  多项式的除法与整数的除法类似。
  （1）把被除式、除式按某个字母作降幂排列，并把所缺的项用零补齐．
  （2）用被除式的第一项去除除式的第一项，得商式的第一项．
  （3）用商式的第一项去乘除式，把积写在被除式下面（同类项对齐），消去相等项，把不相等的项结合起来．
  （4）把减得的差当作新的被除式，再按照上面的方法继续演算，直到余式为零或余式的次数低于除式的次数时为止．
  被除式=除式×商式+余式
  如果一个多项式除以另一个多项式，余式为零，就说这个多项式能被另一个多项式整除
  

考点名称：平方根

• 平方根定义：
  如果一个数的平方等于a，则这个数叫做a的平方根，如果x²=a，那么x叫做a的平方根，这里a是x的平方，它是一个非负数，即a≥0。
  表示：一个正数有两个平方根，用表示平方根中正的那个，用-表示负的平方根。

• 性质：
  ①一个正数如果有平方根，那么必定有两个，它们互为相反数。
  显然，如果我们知道了这两个平方根的一个，那么就可以及时的根据相反数的概念得到它的另一个平方根。

  ②如果一个正数x的平方等于a，即x的平方等于a，那么这个正数x叫做a的算术平方根。a
  的算术平方根记为，读作“根号a”，a叫做被开方数。

  ③规定：0的平方根是0。
  
  ④负数在实数范围内不能开平方，只有在复数范围内，才可以开平方根。
  例如：-1的平方根为±1，-9的平方根为±3。
  
  ⑤平方根包含了算术平方根，算术平方根是平方根中的一种。
  平方根和算术平方根都只有非负数才有。
  被开方数是乘方运算里的幂。
  求平方根可通过逆运算平方来求。
  开平方：求一个非负数a的平方根的运算叫做开平方，其中a叫做被开方数。
  若x的平方等于a，那么x就叫做a的平方根，即正负根号a=正负x

• 1 至 20 的平方根：
  利用长式除法可以求平方根。长式除法需要进行加法，减法，乘法，除法等四则运算。一般计算机软件的运算精度小于20位数字，如要计算平方根到100位，四则运算的精度需100位以上。 利用高精度长式除法可以计算出 1 至 20 的 平方根如下：
  
   1/2    1 2 下一页 尾页

  初中数学考试题
  解答题
  • 最新内容
  • 相关内容
  • 网友推荐
  • 图文推荐

  多项式4x2y-5x3y2+7xy3是（）次（）(2019-03-01)

  下列说法正确的是[]A．整式就是多项(2019-03-01)

  如果m是三次多项式，n是三次多项式(2019-03-01)

  下列说法正确的是[]A.是单项式B.x3(2019-03-01)

  多项式3a2b-a3-1-ab2按字母a的升幂(2019-03-01)

  一次式中b的系数是（），常数项是（(2019-03-01)

  若5x2y|m|-(m+1)y2-3是三次三项式，(2019-03-01)

  若2x-xny+xy+y2-1是关于x、y的3次多(2019-03-01)

  多项式5a2b-4ab+3a-1中，最高次数项(2019-03-01)

  无相关信息

  多项式-15xy2-4x3y的次数和常数项的(2019-03-01)

  已知多项式6a2+mab-ab-10b2除以3a-(2019-03-01)

  把多项式32x3y-45y2+13xy-12x2按照(2019-03-01)

  多项式x3﹣3x2y﹣2x2+5共有（）项，(2019-03-01)

  解方程：（2x+5）（x-1）=2（x+4）(2019-03-01)

  写出一个只含有字母x、y的三次二项(2019-03-01)

  多项式3x|m|+1-（n+1）x+3是二次二(2019-03-01)

  当k=______时，多项式x2-3kxy-3y2-(2019-03-01)

  当x=-10，y=2时，多项式2x-3y+15=_(2019-03-01)

  已知多项式-13x2a+1y-2aa+1y+15xy4(2019-03-01)

  	=1
  	≈1.414213562373095048801688724209698078569671875376948073176679737990732478462
  	≈1.732050807568877293527446341505872366942805253810380628055806979451933016909
  	=2

  多项式-15xy2-4x3y的次数和常

  已知多项式6a2+mab-ab-10b2除

  把多项式32x3y-45y2+13xy-12

  多项式x3﹣3x2y﹣2x2+5共有（

  解方程：（2x+5）（x-1）=2（