(1)计算:2-1+20070+12+1+tan45°;(2)化简求值:(1+1x-1)?(x2-1),其中x=13.(3)在数学上,对于两个数p和q有三种平均数,即算术平均数A、几何平均数G、调和平均数H,其中A=p+q2-数学
题文
(1)计算:2-1+20070+
(2)化简求值:(1+
(3)在数学上,对于两个数p和q有三种平均数,即算术平均数A、几何平均数G、调和平均数H,其中A=
①若p=2,q=6,则A=______,G=______. ②根据上述关系,用p、q的代数式表示出它们的调和平均数H;并根据你所得到的结论,再写出一组调和数. |
答案
(1)原式=
=
=
(2)原式=
=x(x+1), =x2+x, 当x=
(3)①A=
|

![文化广场上摆放了一些长桌子,用于签名支持2008年北京奥运会,假设每张长桌单独摆放时,可容纳6人同时签名[如图(1)],并排摆两张桌子时可容纳10人同时签名[如图(2)].一般地,-数学](http://www.00-edu.com/d/file/ks/shuxue/2/31/2019-03-04/ecc5ef2fc897aa52766c01decaa73022.png)
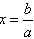
![下面一列数是按照某种规律排列的,…,则第8个数为[]A.B.C.D.-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/31/2019-03-04/8a1f1c9eed4a4e96d3d1da450fb0d2d8.png)

