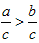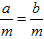若x1、x2都满足条件|2x-1|+|2x+3|=4且x1<x2,则x1-x2的取值范围是______-数学
题文
| 若x1、x2都满足条件|2x-1|+|2x+3|=4且x1<x2,则x1-x2的取值范围是______ |
答案
| |2x-1|+|2x+3|=4,两边都除以2得: |x-
|x+
显然,当x<
而当-
∴-
∴-
上面两式相加:故-2≤x1-x2≤2, 又∵x1<x2,∴x1-x2<0, 故答案为:-2≤x1-x2<0. |
据专家权威分析,试题“若x1、x2都满足条件|2x-1|+|2x+3|=4且x1<x2,则x1-x2的取值范围是..”主要考查你对 一元一次方程的解法,绝对值 等考点的理解。关于这些考点的“档案”如下:
一元一次方程的解法绝对值
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
无相关信息
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |

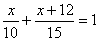
![若=1是方程的解,则的解是[]A.=1B.=0C.=1D.以上都不是-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/35/2019-03-07/49db53d2ecdeccd769003469e566df9a.png)