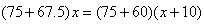创业的故事(1)小王自主创业开了一家服装店,因为进货时没有进行市场调查,在换季时积压了一批服装。为了缓解资金的压力,小王决定打折销售。若每件服装按标价的5折出售将亏2-七年级数学

从左到右依次为:长方形、正方形、三角形、圆、椭圆、
菱形、五边形、六边形。

考点名称:几何体的展开图
- 有些立体图形是由一些平面图形围成的,将它们的表面适当的剪开,可以展开成平面图形,这样的平面图形称为相应立体图形的展开图。
几何体展开图规律:
1.沿多面体的棱将多面体剪开成平面图形,若干个平面图形也可以围成一个多面体;
2.同一个多面体沿不同的棱剪开,得到的平面展开图是不一样的,就是说:同一个立体图形可以有多种不同的展开图。
注意:
①正方体展开头记忆口诀:
正方体盒巧展开,六个面儿七刀裁;
十四条边布周围,十一类图记分明;
四方成线两相卫,六种图形巧组合;
跃马失蹄四分开;两两错开一阶梯。
对面相隔不相连,识图巧排“7”、“凹”、“田”。
②在正方体的展开图中,一条直线上的小正方形不会超过四个。
③正方体的展开图不会有"田"字形,"凹"字形的形状。- 图形展开图:
1.圆柱展开图: →→
→→
2.圆锥展开图: →→
→→
3.长方体展开图: →→
→→
4.正方体展开图: →→
→→
5.三棱柱展开图: →→
→→
6.三棱锥展开图: →→
→→
考点名称:几何体的表面积,体积
- 几何体的表面积和体积要求:
认识柱、锥、台、球及其简单组合体的结构特征,了解柱、锥、台、球的概念;
了解柱、锥、台、球的表面积与体积的计算,并能运用公式计算柱、锥、台、球及其简单组合体的表面积与体积。 - 几何体一般概念及性质:
1、圆柱:可以看做以矩形的一边为旋转轴、旋转一周形成的曲面所围成的几何体
2、圆锥:可以看做以直角三角形的一直角边为旋转轴、旋转一周形成的曲面所围成的几何体
3、圆台:可以看做以直角梯形中垂直于底边的腰所在的直线为旋转轴、旋转一周形成的曲面所围成的几何体
4、球:一个半圆绕着它的直径所在的直线旋转一周所形成的曲面所围成的几何体
5、棱柱有两个面互相平行、而其余每相邻两个面的交线都互相平行
6、多面体是由若干个平面多边形所围成的几何体
7、棱锥有一个面是多边形,而其余个面都是有一个公共顶点的三角形 几何体的表面积,体积计算公式:
1、圆柱体:
表面积:2πRr+2πRh
体积:πR2h (R为圆柱体上下底圆半径,h为圆柱体高)2、圆锥体:
表面积:πR2+πR[(h2+R2)的平方根]
体积: πR2h/3 (r为圆锥体低圆半径,h为其高,3、正方体:
a-边长,
S=6a2 ,V=a34、长方体:
a-长 ,b-宽 ,c-高
S=2(ab+ac+bc) V=abc5、棱柱:
S-底面积 h-高
V=Sh6、棱锥 :
S-底面积 h-高
V=Sh/37、棱台:
S1和S2-上、下底面积 h-高
V=h[S1+S2+(S1S2)^1/2]/38、拟柱体:
S1-上底面积 ,S2-下底面积 ,S0-中截面积 h-高,
V=h(S1+S2+4S0)/69、圆柱:
r-底半径 ,h-高 ,C—底面周长 S底—底面积 ,S侧—侧面积 ,S表—表面积
C=2πr S底=πr2,S侧=Ch ,S表=Ch+2S底 ,V=S底h=πr2h10、空心圆柱:
R-外圆半径 ,r-内圆半径 h-高
V=πh(R^2-r^2)11、直圆锥 :
r-底半径 h-高
V=πr^2h/312、圆台:
r-上底半径 ,R-下底半径 ,h-高
V=πh(R2+Rr+r2)/313、球:
r-半径 d-直径
V=4/3πr^3=πd^3/614、球缺
h-球缺高,r-球半径,a-球缺底半径
V=πh(3a2+h2)/6 =πh2(3r-h)/315、球台:
r1和r2-球台上、下底半径 h-高
V=πh[3(r12+r22)+h2]/616、圆环体:
R-环体半径 D-环体直径 r-环体截面半径 d-环体截面直径
V=2π2Rr2 =π2Dd2/417、桶状体:
D-桶腹直径 d-桶底直径 h-桶高
V=πh(2D2+d2)/12 ,(母线是圆弧形,圆心是桶的中心)
V=πh(2D2+Dd+3d2/4)/15 (母线是抛物线形)
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |