2011年3月10日12时58分,在云南盈江县发生5.8级地震,随后又相继发生里氏4.7级、里氏4.5级、里氏3.6级余震。灾情发生后,全国人民抗震救灾,众志成城。湖州市政府也筹集-七年级数学
题文
2011年3月10日12时58分,在云南盈江县发生5.8级地震,随后又相继发生里氏4.7级、里氏4.5级、里氏3.6级余震。灾情发生后,全国人民抗震救灾,众志成城。湖州市政府也筹集了抗震救灾物资共120吨准备运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
(2)为了节省运费,市政府打算用甲、乙、丙三种车型同时参与运送,已知它们的总车辆数为14辆,你能分别求出三种车型的车辆数吗?此时的运费又是多少元? |
答案
| (1)甲种车型8辆,乙种车型10辆,(2)甲种车型2辆,乙种车型5辆,则丙种车型为7辆,7500元 |
试题分析:(1)首先设需甲车x辆,乙车y辆,根据题意可得两个等量关系:①甲车x辆的运载量+乙车y辆的运载量=120吨,②甲车x辆的运费+乙车y辆的运费=8200元,根据等量关系列出方程,组成方程组,解方程组即可; (2)设甲车有a辆,乙车有b辆,则丙车有(14-a-b)辆,根据运输物资的总量可得5a+8b+10(14-a-b)=120,再根据a、b、14-a-b均为正整数进行讨论计算出b=5,然后算出总运费即可. (1)设需甲车x辆,乙车y辆,由题意得 答:需甲种车型8辆,需乙种车型10辆; (2)设甲车有a辆,乙车有b辆,则丙车有(14-a-b)辆. 由题意,得5a+8b+10(14-a-b)=120, 化简得5a+2b=20,解得 ∵a、b、14-a-b均为正整数, ∴b只能等于5,从而a=2,14-a-b=7, ∴甲车需2辆,乙车需5辆,丙车需7辆, 共需运费400×2+500×5+600×7=7500(元), 答:三种车型的车辆数:甲车需2辆,乙车需5辆,丙车需7辆;共需运费7500元. 点评:解题的关键是找出题目中的等量关系,根据运费和所运物资的总量列出方程求解. |
据专家权威分析,试题“2011年3月10日12时58分,在云南盈江县发生5.8级地震,随后又相继..”主要考查你对 二元一次方程组的定义,二元一次方程的定义,二元一次方程组的解法,二元一次方程组的应用 等考点的理解。关于这些考点的“档案”如下:
二元一次方程组的定义二元一次方程的定义二元一次方程组的解法二元一次方程组的应用
考点名称:二元一次方程组的定义
- 二元一次方程组:
含有两个未知数,并且所含未知数的项的次数都是1的方程叫做二元一次方程。
把两个含有相同未知数的一次方程联合在一起,那么这两个方程就组成了一个二元一次方程组。
二元一次方程组的解:一般的,二元一次方程组的两个二元一次方程的公共解,叫做二元一次方程组的解。
一般形式为: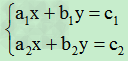 (其中a1,a2,b1,b2不同时为零).
(其中a1,a2,b1,b2不同时为零). - 二元一次方程组的特点:
1.组成二元一次方程组的两个一次方程不一定都是二元一次方程,但这两个方程必须一共含有两个未知数,如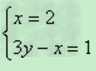 也是二元一次方程组。
也是二元一次方程组。
2.在方程组的每个方程中,相同字母必须代表同一未知量,否则不能将两个方程合在一起。
3.二元一次方程组中的各个方程应是整式方程。
4.二元一次方程组有时也由两个以上的方程组成。 - 二元一次方程与二元一次方程组的区别:
二元一次方程 二元一次方程组 条件 ①含有两个未知数;
②含未知数的项的次数都是1;
③整式方程。①含有两个未知数;
②含未知数的项的次数都是1;
③整式方程组(可任意话说你有两个以上的方程)一般形式 ax+by=c(a、b、c都是常数,且a≠0,b≠0) 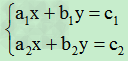
(a1,a2,b1,b2不同时为零).解的情况 无数组解 或无数组解或有唯一解或无解 解的定义 适合二元一次方程的每一对未知数的值,叫做这个二元一次方程的一组解 二元一次方程组中各个方程的公共解叫做这个二元一次方程组的解 二元一次方程组的判定:
①方程组各方程中,相同的字母必须代表同一数量,否则不能将两个方程合在一起.
②怎样检验一组数值是不是某个二元一次方程组的解,常用的方法如下:将这组数值分别代入方程组中的每个方程,只有当这组数值满足其中的所有方程时,才能说这组数值是此方程组的解,否则,如果这组数值不满足其中任一个方程,那么它就不是此方程组的解.
考点名称:二元一次方程的定义
- 二元一次方程:
如果一个方程含有两个未知数,并且所含未知项都为1次方,那么这个整式方程就叫做二元一次方程,有无穷个解,若加条件限定有有限个解。二元一次方程组,则一般有一个解,有时没有解,有时有无数个解。
二元一次方程的一般形式:ax+by+c=0其中a、b不为零。
二元一次方程的解:使二元一次方程左、右两边的值相等的一对未知数的值,叫做二元一次方程的一个解 。 - 二元一次方程的特点:
1.在方程中“元”是指未知数,“二元”是指方程中有且只有两个未知数。
2.未知数的项的次数是1,指的是含有未知数的项(单项式)的次数是1,如3xy的次数是2,所以方程3xy-2=0不是二元一次方程。
3.二元一次方程的左边和右边都必须是整式,例如方程1/x-y=1的左边不是整式,所以她不是二元一次方程。
二元一次方程的解的特点:
1.二元一次方程的每个解都包括两个未知数的值,是一对数值,而不是一个数值,如x=7不是方程x+y=18的一个解,而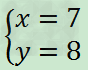 才是方程x+y=18的一个解。
才是方程x+y=18的一个解。
2.二元一次方程的解是具有相关性的一对未知数的值,二者相互制约,相互对应,不独立存在,当其中一个未知数的值确定以后,另一个未知数的值也确定了。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
无相关信息
上一篇:解方程组:-七年级数学
下一篇:某家电商场计划用9万元从生产厂家购进50台电视机.已知该厂家生产3种不同型号的电视机,出厂价分别为A种每台1500元,B种每台2100元,C种每台2500元.(1)若家电商场同时购进两-七年级数学
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |

![下列方程组中,属于二元一次方程组的是[]A、B、C、D、-八年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/43/2019-03-11/b36bfe623df29122a185159d4b57838b.gif)

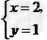
![下列方程组中,是二元一次方程组的是[]-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/43/2019-03-12/c61b1fc773738575f4db7b7f2daa9802.png)

