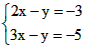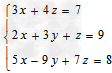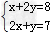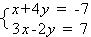检验方程组的解时,必须将求得的未知数的值代入方程组中的每一个方程.例1:解方程组x+y=4x+y3-x2=1思路分析:本例这两个方程中①较简单,且x、y的系数均为1,故可把①变形,把x用-数学
题文
| 检验方程组的解时,必须将求得的未知数的值代入方程组中的每一个方程. 例1:解方程组
思路分析:本例这两个方程中①较简单,且x、y的系数均为1,故可把①变形,把x用y表示,或把y用x来表示皆可,然后将其代入②,消去一个未知数,化成一元一次方程,进而再求出方程组的解. 把①变形为y=4-x ③ 把③代入②得:
即
∴x=
把x=
所以原方程的解是
若想知道解的是否正确,可作如下检验: 检验:把x=
所以左边=右边. 再把x=
左边
|

![若方程组的解x,y满足0<x+y<1,则k的取值范围是[]A.-4<k<0B.-1<k<0C.0<k<8D.k>-4-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/44/2019-03-13/a7d61c64fe1e7b6c90f32ce7d9106b67.png)