某工厂工人的工作时间为每月25天,每天8小时,该厂生产A、B两种产品,每位工人每月有基本工资400元,工人每生产一件A种产品,可得报酬0.75元,每生产一件B种产品,可得报酬-九年级数学
题文
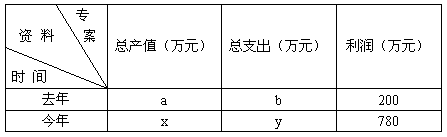
| 某工厂工人的工作时间为每月25天,每天8小时,该厂生产A、B两种产品,每位工人每月有基本工资400元,工人每生产一件A种产品,可得报酬0.75元,每生产一件B种产品,可得报酬1.40元,下表记录了工人小李的工作情况: | |||||||||
(2)求小李每月工资额的范围。 |
答案
| 解:(1)设小李每生产一件A种、B种产品分别需要x、y分钟 则  解得  故小李每生产一件A种和B种产品需要的时间分别为15分钟,20分钟。 (2)设小李每月生产A、B两种产品的件数分别为m、n,月工资额为了w 则  即  因为m,n为非负整数, 所以0≤m≤800 故当m=0时,w有最大值为1240, 当m=800时,w有最小值为1000, ∴小李月工资额的范围在1000元至1240元之间(包含1000元,1240元)。 |
据专家权威分析,试题“某工厂工人的工作时间为每月25天,每天8小时,该厂生产A、B两种产..”主要考查你对 二元一次方程组的应用 等考点的理解。关于这些考点的“档案”如下:
二元一次方程组的应用
考点名称:二元一次方程组的应用
- 二元一次方程组应用中常见的相等关系:
1. 行程问题(匀速运动)
基本关系:s=vt
①相遇问题(同时出发):
确定行程过程中的位置路程
相遇路程÷速度和=相遇时间
相遇路程÷相遇时间= 速度和
相遇问题(直线)
甲的路程+乙的路程=总路程
相遇问题(环形)
甲的路程 +乙的路程=环形周长
②追及问题(同时出发):
追及时间=路程差÷速度差
速度差=路程差÷追及时间
追及时间×速度差=路程差
追及问题(直线)
距离差=追者路程-被追者路程=速度差X追及时间
追及问题(环形)
快的路程-慢的路程=曲线的周长
③水中航行
顺水行程=(船速+水速)×顺水时间
逆水行程=(船速-水速)×逆水时间
顺水速度=船速+水速
逆水速度=船速-水速
静水速度=(顺水速度+逆水速度)÷2
水速:(顺水速度-逆水速度)÷2
2.配料问题:溶质=溶液×浓度
溶液=溶质+溶剂
3.增长率问题
4.工程问题
基本关系:工作量=工作效率×工作时间(常把工作量看成单位“1”)。
5.几何问题
①常用勾股定理,几何体的面积、体积公式,相似形及有关比例性质等。
②注意语言与解析式的互化:
如,“多”、“少”、“增加了”、“增加为(到)”、“同时”、“扩大为(到)”、“扩大了”、……
又如,一个三位数,百位数字为a,十位数字为b,个位数字为c,则这个三位数为:100a+10b+c,而不是abc。
③注意从语言叙述中写出相等关系:
如,x比y大3,则x-y=3或x=y+3或x-3=y。又如,x与y的差为3,则x-y=3。
④注意单位换算:
如,“小时”“分钟”的换算;s、v、t单位的一致等。 二元一次方程组的应用:
列方程(组)解应用题是中学数学联系实际的一个重要方面。
其具体步骤是:
⑴审题。理解题意。弄清问题中已知量是什么,未知量是什么,问题给出和涉及的相等关系是什么。
⑵设元(未知数)。①直接未知数②间接未知数(往往二者兼用)。一般来说,未知数越多,方程越易列,但越难解。
⑶用含未知数的代数式表示相关的量。
⑷寻找相等关系(有的由题目给出,有的由该问题所涉及的等量关系给出),列方程。一般地,未知数个数与方程个数是相同的。
⑸解方程及检验。
⑹答案。
综上所述,列方程(组)解应用题实质是先把实际问题转化为数学问题(设元、列方程),在由数学问题的解决而导致实际问题的解决(列方程、写出答案)。在这个过程中,列方程起着承前启后的作用。因此,列方程是解应用题的关键。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |

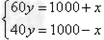
![有6个班的同学在学校礼堂听报告,若每条长凳坐4人,还缺3条长凳;若每条长凳坐6人,就多1条长凳,设同学有x人,礼堂共有y条长凳,下列所列方程组正确的是[]A.B.C.D.-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/45/2019-03-15/4103c1aa75cca4c6a009a0536c24ee1f.gif)

