2010年4月14日7时49分在我国青海省玉树发生里氏7、1级的强烈地震,灾情牵动全国人民的心,“大爱无疆,心系玉树”.某地区计划为灾人民区搭建A、B两种型号的帐篷300顶,其中A型-数学
题文
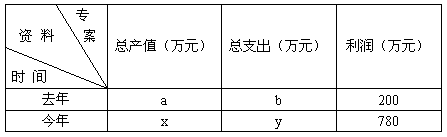
| 2010年4月14日7时49分在我国青海省玉树发生里氏7、1级的强烈地震,灾情牵动全国人民的心,“大爱无疆,心系玉树”.某地区计划为灾人民区搭建A、B两种型号的帐篷300顶,其中A型帐篷可供3人居住;B型帐篷可供10人居住,正好可供2300人临时居住. (1)求该地区搭建A型、B型帐篷各多少间? (2)该地区计划租用甲乙两种型号的卡车共20辆将这批帐篷紧急送往灾区,已知甲型卡车每辆可同时装运4顶A帐篷和11顶B帐篷;乙型卡车每辆可同时装运12顶A帐篷和7顶B帐篷.能否安排甲乙两种卡车恰好一次性将这批帐篷送往灾区?如果不能,请你说出一种方案把这批帐篷一次性运往灾区(只要写出一种即可)? |

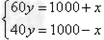
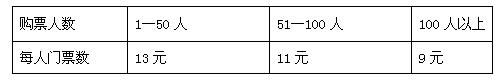
![有6个班的同学在学校礼堂听报告,若每条长凳坐4人,还缺3条长凳;若每条长凳坐6人,就多1条长凳,设同学有x人,礼堂共有y条长凳,下列所列方程组正确的是[]A.B.C.D.-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/45/2019-03-15/4103c1aa75cca4c6a009a0536c24ee1f.gif)

