周末某班组织登山活动,同学们分甲、乙两组从山脚下沿着一条道路同时向山顶进发,设甲、乙两组行进同一段路程所用的时间之比为2:3。(1)直接写出甲、乙两组行进速度之比;(2)-七年级数学
题文
| 周末某班组织登山活动,同学们分甲、乙两组从山脚下沿着一条道路同时向山顶进发,设甲、乙两组行进同一段路程所用的时间之比为2:3。 (1)直接写出甲、乙两组行进速度之比; (2)当甲组到达山顶时,乙组行进到山腰A处,且A 处离山顶的路程尚有1.2千米,试问山脚离山顶的 路程有多远? (3)在题(2)所述内容(除最后的问句外)的基础上,设乙组从A处继续登山,甲组到达山顶后,休息片刻,再从原路下山,并且在山腰B处与乙组相遇,请你先根据以上情景提出一个相应的问题,再给予解答。(要求:①问题的提出不得再增添其他条件; ②问题的解决必须利用上述情景提供的所有已知条件) |
答案
| 解:(1)甲、乙两组的行进速度之比为3:2; (2)山脚离山顶路程为3.6千米; (3)略。 |
据专家权威分析,试题“周末某班组织登山活动,同学们分甲、乙两组从山脚下沿着一条道路..”主要考查你对 二元一次方程的应用,一元一次方程的应用 等考点的理解。关于这些考点的“档案”如下:
二元一次方程的应用一元一次方程的应用
考点名称:二元一次方程的应用
- 定义的应用,判定一个方程是否是二元一次方程;求方程的未知系数及解应用题。
列二元一次方程组解应用题的一般步骤:
可概括为“审、找、列、解、答”五步,即:
(1)审:通过审题,把实际问题抽象成数学问题,分析已知数和未知数,并用字母表示其中的两个未知数;
(2)找:找出能够表示题意两个相等关系;
(3)列:根据这两个相等关系列出必需的代数式,从而列出方程组;
(4)解:解这个方程组,求出两个未知数的值;
(5)答:在对求出的方程的解做出是否合理判断的基础上,写出答案.
常见问题及解决:
一、数字问题:
例:一个两位数,比它十位上的数与个位上的数的和大9;如果交换十位上的数与个位上的数,所得两位数比原两位数大27,求这个两位数.
分析:设这个两位数十位上的数为x,个位上的数为y,则这个两位数及新两位数及其之间的关系表示为: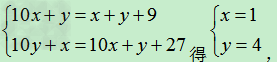 因此,所求的两位数是14.
因此,所求的两位数是14.
点评:由于受一元一次方程先入为主的影响,不少同学习惯于只设一元,然后列一元一次方程求解,虽然这种方法十有八九可以奏效,但对有些问题是无能为力的,象本题,如果直接设这个两位数为x,或只设十位上的数为x,那将很难或根本就想象不出关于x的方程.一般地,与数位上的数字有关的求数问题,一般应设各个数位上的数为“元”,然后列多元方程组解之.
二、利润问题:
商品销售盈利百分数是相对于进价而言的,不要误为是相对于定价或卖出价.
利润的计算一般有两种方法:
①利润=卖出价-进价;
②利润=进价×利润率(盈利百分数)。
特别注意“利润”和“利润率”是不同的两个概念。
三、配套问题:
产品配套是工厂生产中基本原则之一,如何分配生产力,使生产出来的产品恰好配套成为主管生产人员常见的问题,解决配套问题的关键是利用配套本身所存在的相等关系,其中两种最常见的配套问题的等量关系是:
①“二合一”问题:如果a件甲产品和b件乙产品配成一套,
那么甲产品数的b倍等于乙产品数的a倍,即: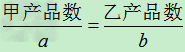 ;
;
②“三合一”问题:如果甲产品a件,乙产品b件,丙产品c件配成一套,
那么各种产品数应满足的相等关系式是: 。
。
四、行程问题:
“相向而遇”和“同向追及”是行程问题中最常见的两种题型,在这两种题型中都存在着一个相等关系,这个关系涉及到两者的速度、原来的距离以及行走的时间,具体表现在:
“相向而遇”时,两者所走的路程之和等于它们原来的距离;
“同向追及”时,快者所走的路程减去慢者所走的路程等于它们原来的距离。
五、货运问题:
由实际问题列出的方程组一般都可以再化简,因此,解实际问题的方程组时要注意先化简,再考虑消元和解法,这样可以减少计算量,增加准确度.化简时一般是去分母或两边同时除以各项系数的最大公约数或移项、合并同类项等。
六、工程问题:
工程问题与行程问题相类似,关键要抓好三个基本量的关系,即
“工作量=工作时间×工作效率”以及它们的变式:
“工作时间=工作量÷工作效率,
工作效率=工作量÷工作时间”。
其次注意当题目与工作量大小、多少无关时,通常用“1”表示总工作量。
考点名称:一元一次方程的应用
- 许多实际问题都归结为解一种方程或方程组,所以列出方程或方程组解应用题是数学联系实际,解决实际问题的一个重要方面;
同时通过列方程解应用题,可以培养我们分析问题,解决问题的能力。 - 列一元一次方程解应用题的一般步骤:
列方程(组)解应用题是中学数学联系实际的一个重要方面。其具体步骤是:
⑴审题:理解题意。弄清问题中已知量是什么,未知量是什么,问题给出和涉及的相等关系是什么。
⑵设元(未知数):找出等量关系:找出能够表示本题含义的相等关系;
①直接未知数:设出未知数,列出方程:设出未知数后,表示出有关的含字母的式子,然后利用已找出的等量关系列出方程;
②间接未知数(往往二者兼用)。
一般来说,未知数越多,方程越易列,但越难解。
⑶用含未知数的代数式表示相关的量。
⑷寻找相等关系(有的由题目给出,有的由该问题所涉及的等量关系给出),列方程。一般地,未知数个数与方程个数是相同的。
⑸解方程及检验。
⑹答题。
综上所述,列方程(组)解应用题实质是先把实际问题转化为数学问题(设元、列方程),在由数学问题的解决而导致实际问题的解决(列方程、写出答案)。在这个过程中,列方程起着承前启后的作用。因此,列方程是解应用题的关键。 一元一次方程应用题型及技巧:
列方程解应用题的几种常见类型及解题技巧:
(1)和差倍分问题:
①倍数关系:通过关键词语“是几倍,增加几倍,增加到几倍,增加百分之几,增长率……”来体现。
②多少关系:通过关键词语“多、少、和、差、不足、剩余……”来体现。
③基本数量关系:增长量=原有量×增长率,现在量=原有量+增长量。
(2)行程问题:
基本数量关系:路程=速度×时间,时间=路程÷速度,速度=路程÷时间,
路程=速度×时间。
①相遇问题:快行距+慢行距=原距;
②追及问题:快行距-慢行距=原距;
③航行问题:
顺水(风)速度=静水(风)速度+水流(风)速度,
逆水(风)速度=静水(风)速度-水流(风)速度
例:甲、乙两站相距480公里,一列慢车从甲站开出,每小时行90公里,一列快车从乙站开出,每小时行140公里。
慢车先开出1小时,快车再开。两车相向而行。问快车开出多少小时后两车相遇?
两车同时开出,相背而行多少小时后两车相距600公里?
两车同时开出,慢车在快车后面同向而行,多少小时后快车与慢车相距600公里?
两车同时开出同向而行,快车在慢车的后面,多少小时后快车追上慢车?
慢车开出1小时后两车同向而行,快车在慢车后面,快车开出后多少小时追上慢车? (此题关键是要理解清楚相向、相背、同向等的含义,弄清行驶过程。)
例: 一艘船在两个码头之间航行,水流速度是3千米每小时,顺水航行需要2小时,逆水航行需要3小时,求两码头的之间的距离?<?xml:namespace prefix = "o" ns = "urn:schemas-microsoft-com:office:office" />(3)劳力分配问题:抓住劳力调配后,从甲处人数与乙处人数之间的关系来考虑。 这类问题要搞清人数的变化。
例.某厂一车间有64人,二车间有56人。现因工作需要,要求第一车间人数是第二车间人数的一半。问需从第一车间调多少人到第二车间?
(4)工程问题:
三个基本量:工作量、工作时间、工作效率;
其基本关系为:工作量=工作效率×工作时间;相关关系:各部分工作量之和为1。
例:一件工程,甲独做需15天完成,乙独做需12天完成,现先由甲、乙合作3天后,甲有其他任务,剩下工程由乙单独完成,问乙还要几天才能完成全部工程?
(5)利润问题:
基本关系:
①商品利润=商品售价-商品进价;
②商品利润率=商品利润/商品进价×100%;
③商品销售额=商品销售价×商品销售量;
④商品的销售利润=(销售价-成本价)×销售量。
⑤商品售价=商品标价×折扣率例.
例:一家商店将某种服装按进价提高40%后标价,又以8折优惠卖出,结果每件仍获利15元,这种服装每件的进价是多少?
(6)数字问题:一般可设个位数字为a,十位数字为b,百位数字为c,十位数可表示为10b+a, 百位数可表示为100c+10b+a,然后抓住数字间或新数、原数之间的关系找等量关系列方程。
数字问题中一些表示:两个连续整数之间的关系,较大的比较小的大1;
偶数用2n表示,连续的偶数用2n+2或2n—2表示;奇数用2n+1或2n—1表示。
例:有一个三位数,个位数字为百位数字的2倍,十位数字比百位数字大1,若将此数个位与百位顺序对调(个位变百位)所得的新数比原数的2倍少49,求原数。
(7)盈亏问题:“盈”表示分配中的多余情况;“亏”表示不足或缺少部分。
(8)储蓄问题:
其数量关系是:
利息=本金×利率×存期;:(注意:利息税)。
本息=本金+利息,利息税=利息×利息税率。
注意利率有日利率、月利率和年利率,年利率=月利率×12=日利率×365。
(9)溶液配制问题:
其基本数量关系是:溶液质量=溶质质量+溶剂质量;
溶质质量=溶液中所含溶质的质量分数。
这类问题常根据配制前后的溶质质量或溶剂质量找等量关系,分析时可采用列表的方法来帮助理解题意。(10)比例分配问题:
这类问题的一般思路为:设其中一份为x,利用已知的比,写出相应的代数式。
常用等量关系:各部分之和=总量。
还有劳力调配问题、配套问题、年龄问题、比赛积分问题、增长率问题等都会有涉及。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |