在方程3x-2y=4中,用含y的代数式表示x为:______;用含x的代数式表示y为:______.-数学
题文
| 在方程3x-2y=4中,用含y的代数式表示x为:______;用含x的代数式表示y为:______. |
答案
| 3x-2y=4, 解得:x=
故答案为:x=
|
据专家权威分析,试题“在方程3x-2y=4中,用含y的代数式表示x为:______;用含x的代数式表..”主要考查你对 二元一次方程的解法 等考点的理解。关于这些考点的“档案”如下:
二元一次方程的解法
考点名称:二元一次方程的解法
- 二元一次方程的解:
使二元一次方程左、右两边的值相等的一对未知数的值,叫做二元一次方程的一个解。 二元一次方程解法:
二元一次方程有无数个解,除非题目中有特殊条件。
一、消元法
“消元”是解二元一次方程的基本思路。所谓“消元”就是减少未知数的个数,使多元方程最终转化为一元方程再解出未知数。这种将方程组中的未知数个数由多化少,逐一解决的想法,叫做消元思想。
如:5x+6y=7 2x+3y=4,变为5x+6y=7 4x+6y=8
消元方法:
代入消元法(常用)
加减消元法(常用)
顺序消元法(这种方法不常用)
例:
x-y=3 ①
{
3x-8y=4②
由①得x=y+3③
③代入②得
3(y+3)-8y=4
y=1
所以x=4
则:这个二元一次方程组的解
x=4
{
y=1(一)加减-代入混合使用的方法.
例:
13x+14y=41 ①
{
14x+13y=40②
②-①得
x-y=-1
x=y-1 ③
把③代入①得
13(y-1)+14y=41
13y-13+14y=41
27y=54
y=2
把y=2代入③得
x=1
所以:x=1,y=2
最后 x=1 ,y=2, 解出来
特点:两方程相加减,得到单个x或单个y,适用接下来的代入消元。(二)代入法
是二元一次方程的另一种方法,就是说把一个方程带入另一个方程中
如:
x+y=590
y+20=90%x
带入后就是:
x+90%x-20=590
(x+5)+(y-4)=8
(x+5)-(y-4)=4
令x+5=m,y-4=n
原方程可写为
m+n=8
m-n=4
解得m=6,n=2
所以x+5=6,y-4=2
所以x=1,y=6
特点:两方程中都含有相同的代数式(x+5,y-4),换元后可简化方程。(三)另类换元
例:
x:y=1:4①
5x+6y=29②
令x=t,y=4t
方程2可写为:5t+24t=29
29t=29
t=1
所以x=1,y=4二、换元法
解数学题时,把某个式子看成一个整体,用一个变量去代替它,从而使问题得到简化,这叫换元法。换元的实质是转化,关键是构造元和设元,理论依据是等量代换,目的是变换研究对象,将问题移至新对象的知识背景中去研究,从而使非标准型问题标准化、复杂问题简单化,变得容易处理。
换元法又称辅助元素法、变量代换法。通过引进新的变量,可以把分散的条件联系起来,隐含的条件显露出来,或者把条件与结论联系起来。或者变为熟悉的形式,把复杂的计算和推证简化。
它可以化高次为低次、化分式为整式、化无理式为有理式、化超越式为代数式,在研究方程、不等式、函数、数列、三角等问题中有广泛的应用。
如:
(x+y)/2-(x-y)/3=6
3(x+y)=4(x-y)
解:
设x+y为a,x-y为b
原=a/2-b/3=6①
3a=4b②
①×6 得3a-2b=36③
把②代入③ 得2b=36 b=18
把b=18代入②得a=24
所以x+y=24④
x-y=18⑤
④-⑤得 2y=6 y=3
把y=3代入④得 x=21
x=21,y=3
是方程组的解
整体代入
如:
2x+5y=15①
85-7y=2x②
解:把②代入①得
85-7y+5y=15
-2y=-70
y=35
把y=35代入②
得x=-80
x=-80,y=35
是方程组的解二元一次方程有两个正根的特点:
二元一次方程ax2+bx+c=0(a≠0)
有两个正跟要满足下列3个条件
1、保证有两个跟,即:△≥0,也就是b2-4ac≥0
2、x1+x2>0,即 —b/a>0
3、x1×x2>0,即c/a>0
然后根据所给的条件在求出题目中要求的某些字母的值
二元一次方程整数解存在的条件:
在整系数方程ax+by=c中,
若a,b的最大公约数能整除c,则方程有整数解。即
如果(a,b)|c 则方程ax+by=c有整数解
显然a,b互质时一定有整数解。
例如方程
3x+5y=1,
5x-2y=7,
9x+3y=6都有整数解。
返过来也成立,方程
9x+3y=10和
4x-2y=1都没有整数解,
∵(9,3)=3,而3不能整除10;
(4,2)=2,而2不能整除1。
一般我们在正整数集合里研究公约数,(a,b)中的a,b实为它们的绝对值。
二元一次方程整数解的方法:
①首先用一个未知数表示另一个未知数,如y=10-2x;
②给定x一个值,求y的一个对应值,就可以得到二元一次方程的一组解;
③根据提议对未知数x、y做出限制,确定x的可能取值,确定二元一次方程所有的整数解。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |

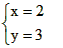
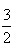
![已知是方程mx﹣y=﹣3的解,那么m的值是[]A.2B.﹣2C.1D.﹣1-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/47/2019-03-16/106d7dcef91998e830a0b3bffd26be0b.png)
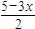
![设是方程3x﹣y=0的一个解,那么[]A.a,b一定都是正数B.a,b一定都是负数C.a,b必同为0D.a,b不可能异号-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/47/2019-03-16/169f71c2eb88cbb037c7190b501e595e.png)
