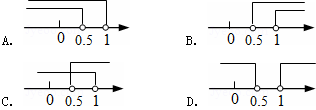
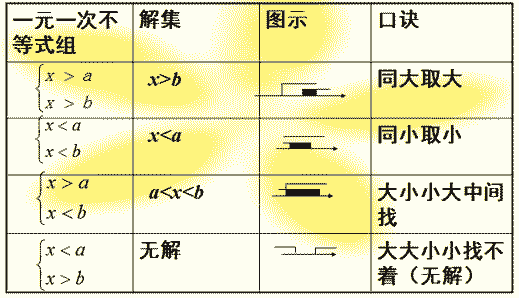
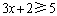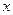已知平面直角坐标系上的动点A(x,y),满足x=1+2a,y=1-a,其中-3≤a≤1,有下列四个结论:①-5≤x≤3,②-4≤y≤0,③-9≤x+y≤3,④若x≤0,则32≤y≤4.其中正确的结论个数是()A.0个B.1个C.-数学
题文
已知平面直角坐标系上的动点A(x,y),满足x=1+2a,y=1-a,其中-3≤a≤1,有下列四个结论:①-5≤x≤3,②-4≤y≤0,③-9≤x+y≤3,④若x≤0,则
|
答案
| ①在不等式-3≤a≤1的两边同时乘以2,得 -6≤2a≤2, 在不等式的两边同时加上1,得 -5≤1+2a≤3,即-5≤x≤3. 故①正确; ②在不等式-3≤a≤1的两边同时乘以-1,得 3≥-a≥-1, 在不等式的两边同时加上1,得 4≥1-a≥0,即0≤y≤4. 故②错误; ③由①②知,-5≤x≤3,0≤y≤4, ∴-5≤x+y≤7. 故③错误; ④若x≤0时,1+2a≤0,解得,a≤-
又∵-3≤a≤1, ∴-3≤a≤-
∴
故④正确; 综上所述,正确的结论是:①④,共有2个. 故选C. |
据专家权威分析,试题“已知平面直角坐标系上的动点A(x,y),满足x=1+2a,y=1-a,其中-3..”主要考查你对 不等式的性质 等考点的理解。关于这些考点的“档案”如下:
不等式的性质
考点名称:不等式的性质
- 不等式的性质:
1、不等式的基本性质:
不等式性质1:不等式的两边同时加上(或减去)同一个数(或式子),不等号的方向不变。即如果a>b,那么a±c>b±c。
不等式性质2:不等式的两边同时乘(或除以)同一个正数,不等号的方向不变。即如果a>b,c>0,那么ac>bc(或 )。
)。
不等式性质3:不等式的两边同时乘(或除以)同一个负数,不等号的方向改变。即如果a>b,c<0,那么ac<bc(或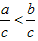 )。
)。
2、不等式的互逆性:若a>b,则b<a。
3、不等式的传递性:若a>b,b>c,则a>c。 不等式的性质:
①如果x>y,那么y<x;如果y<x,那么x>y;(对称性)
②如果x>y,y>z;那么x>z;(传递性)
③如果x>y,而z为任意实数或整式,那么x+z>y+z;(加法原则,或叫同向不等式可加性)
④ 如果x>y,z>0,那么xz>yz;如果x>y,z<0,那么xz<yz;(乘法原则)
⑤如果x>y,z>0,那么x÷z>y÷z;如果x>y,z<0,那么x÷z<y÷z;
⑥如果x>y,m>n,那么x+m>y+n;(充分不必要条件)
⑦如果x>y>0,m>n>0,那么xm>yn;
⑧如果x>y>0,那么x的n次幂>y的n次幂(n为正数),x的n次幂<y的n次幂(n为负数)
或者说,不等式的基本性质有:
①对称性;
②传递性:
③加法单调性:即同向不等式可加性:
④乘法单调性:
⑤同向正值不等式可乘性:
⑥正值不等式可乘方:
⑦正值不等式可开方:
⑧倒数法则。- 不等式的基本性质和等式的基本性质的异同:
①相同点:无论是等式还是不等式,都可以在它的两边加(或减)同一个数或同一个整式;
②不同点:对于等式来说,在等式的两边乘(或除以)同一个正数(或同一个负数),等式仍然成立,但是对于不等式来说,却不大一样,在不等式的两边乘(或除以)同一个正数,不等号的方向不变,而在不等式的两边乘(或除以)同一个负数,不等号要改变方向。 原理:
①不等式F(x)< G(x)与不等式 G(x)>F(x)同解。
②如果不等式F(x) < G(x)的定义域被解析式H( x )的定义域所包含,那么不等式 F(x)<G(x)与不等式F(x)+H(x)<G(x)+H(x)同解。
③如果不等式F(x)<G(x) 的定义域被解析式H(x)的定义域所包含,并且H(x)>0,那么不等式F(x)<G(x)与不等式H(x)F(x)<H( x )G(x) 同解;如果H(x)<0,那么不等式F(x)<G(x)与不等式H (x)F(x)>H(x)G(x)同解。
④不等式F(x)G(x)>0与不等式同解;不等式F(x)G(x)<0与不等式同解。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |