题文

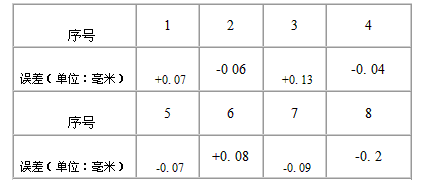
有两种蠓虫，一种是疾病的媒介，记为A；另一种却是有益的花粉传播者，记为B．现有A、B两种蠓虫各6只，它们的触角和翼的长度列如图： A种 B种 翼长 触角 翼长 触角  1.78  1.14  1.72  1.24  1.86  1.20  1.74  1.36  1.96  1.18  1.70  1.41  2.00  1.28  1.82  1.38  2.00  1.28  1.82  1.48  1.86  1.29  1.82  1.50 ①记6只A种蠓虫的平均翼长、触角长分别为A1和A2，6只B种蠓虫的平均翼长、触角长分别为B1和B2，问|A1-B1|+|A2-B2|等于______． ②对于一只新扑捉到的蠓虫，记其翼长、触角分别为x和y．如果|x-A1|+|y-A2|＞|x-B1|+|x-B2|，则认为它是A种蠓虫，否则认为它是B种蠓虫．现知，x=1.80，y=1.24，则可认为该蠓虫是______种蠓虫．

题型：填空题  难度：中档

答案

①从上表可以得出 A1= 1.78+1.86+1.96+2.00+2.00+1.86 6 =1.91 A2= 1.14+1.2+1.18+1.28+1.28+1.29 6 =1.23 B1= 1.72+1.74+1.70+1.82+1.82+1.82 6 =1.77 B2= 1.24+1.36+1.41+1.38+1.48+1.50 6 =1.40 ∴|A1-B1|+|A2-B2|=0.14+0.17=0.31． ②将x=1.80，y=1.24代入|x-A1|+|y-A2| |x-A1|+|y-A2|=0.11+0.01=0.12 将x=1.80，y=1.24代入|x-B1|+|x-B2| |x-B1|+|x-B2|=0.03+0.16=0.19 ∵0.12＜0.19 ∴可认为该蠓虫是B种蠓虫

据专家权威分析，试题“有两种蠓虫，一种是疾病的媒介，记为A；另一种却是有益的花粉传播..”主要考查你对  绝对值，平均数  等考点的理解。关于这些考点的“档案”如下：

绝对值平均数

考点名称：绝对值

• 绝对值定义：
  在数轴上，表示一个数的点到原点的距离叫做这个数的绝对值。
  绝对值用“||”来表示。
  在数轴上，表示一个数a的点到数b的点之间的距离的值，叫做a-b的绝对值，记作|a-b|。

• 绝对值的意义：
  1、几何的意义：
  在数轴上，一个数到原点的距离叫做该数的绝对值．如：5指在数轴上表示数5的点与原点的距离，这个距离是5，所以5的绝对值是5。
  
  2、代数的意义：
  非负数（正数和0,）
  非负数的绝对值是它本身，非正数的绝对值是它的相反数。
  互为相反数的两个数的绝对值相等。
  a的绝对值用“|a |”表示．读作“a的绝对值”。
  实数a的绝对值永远是非负数，即|a |≥0。
  互为相反数的两个数的绝对值相等，即|-a|=|a|。
  若a为正数，则满足|x|=a的x有两个值±a，如|x|=3，,则x=±3.

• 绝对值的有关性质：
  ①任何有理数的绝对值都是大于或等于0的数，这是绝对值的非负性；
  ②绝对值等于0的数只有一个，就是0；
  ③绝对值等于同一个正数的数有两个，这两个数互为相反数；
  ④互为相反数的两个数的绝对值相等。
  
  绝对值的化简：
  绝对值意思是值一定为正值，按照“符号相同为正，符号相异为负”的原则来去绝对值符号。
  ①绝对值符号里面为负，在去掉绝对值时必须要加一个负的符号老确保整个值为正值，也就是当：
  │a│=a (a为正值，即a≥0 时）；│a│=-a （a为负值，即a≤0 时）
  ②整数就找到这两个数的相同因数；
  ③小数就把这两个数同时扩大相同倍数成为整数,一般都是扩大10、100倍；
  ④分数的话就相除，得数是分数就是分子：分母，要是得数是整数，就这个数比1。

考点名称：平均数

• 平均数：
  是指在一组数据中所有数据之和再除以数据的个数。平均数是表示一组数据集中趋势的量数，它是反映数据集中趋势的一项指标。
  解答平均数应用题的关键在于确定“总数量”以及和总数量对应的总份数。
  在统计工作中，平均数(均值)和标准差是描述数据资料集中趋势和离散程度的两个最重要的测度值。

• 平均数的分类:
  （1）算术平均数：一般地，如果有n个数 ，那么 ，叫做这n个数的算术平均数。
  （2）加权平均数：一组数据点的权分别为，那么称为这n个数的加权平均数。
  （3）样本平均数：样本中所有个体的平均数。
  （4）总体平均数：总体中所有个体的平均数，统计学中常用样本的平均数估计总体的平均数。

• 平均数、中位数和众数关系:
  联系:
           平均数、中位数和众数都是来刻画数据平均水平的统计量，它们各有特点。对于平均数大家比较熟悉，中位数刻画了一组数据的中等水平，众数刻画了一组数据中出现次数最多的情况。
          平均数非常明显的优点之一是，它能够利用所有数据的特征，而且比较好算。另外，在数学上，平均数是使误差平方和达到最小的统计量，也就是说利用平均数代表数据，可以使二次损失最小。因此，平均数在数学中是一个常用的统计量。但是平均数也有不足之处，正是因为它利用了所有数据的信息，平均数容易受极端数据的影响。
           例如，在一个单位里，如果经理和副经理工资特别高，就会使得这个单位所有成员工资的平均水平也表现得很高，但事实上，除去经理和副经理之外，剩余所有人的平均工资并不是很高。这时，中位数和众数可能是刻画这个单位所有人员工资平均水平更合理的统计量。
          中位数和众数这两个统计量的特点都是能够避免极端数据，但缺点是没有完全利用数据所反映出来的信息。
          由于各个统计量有各自的特征，所以需要我们根据实际问题来选择合适的统计量。
          当然，出现极端数据不一定用中位数，一般，统计上有一个方法，就要认为这个数据不是来源于这个总体的，因而把这个数据去掉。比如大家熟悉的跳水比赛评分，为什么要去掉一个最高分、一个最低分呢，就认为这两个分不是来源于这个总体，不能代表裁判的鉴赏力。于是去掉以后再求剩下数据的平均数。需要指出的是，我们处理的数据，大部分是对称的数据，数据符合或者近似符合正态分布。这时候，均值(平均数)、中位数和众数是一样的。

  区别:
          只有在数据分布偏态(不对称)的情况下，才会出现均值、中位数和众数的区别。所以说，如果是正态的话，用哪个统计量都行。如果偏态的情况特别严重的话，可以用中位数。
           除了需要刻画平均水平的统计量，统计中还有刻画数据波动情况的统计量。比如，平均数同样是5，它所代表的数据可能是1、3、5、7、9，可能是4、4.5、5、5.5、6。也就是说5所代表的不同组数据的波动情况是不一样的。怎样刻画数据的波动情况呢?很自然的想法就是用最大值减最小值，即求一组数据的极差。数学中还有方差、标准差等许多用来刻画数据特征的统计量。当然这些都是教师感兴趣、值得了解的内容，不是小学数学的教学要求。