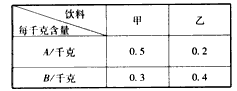
某商场准备进一批不同型号的衣服,若购进A种型号衣服5件,B种型号衣服3件,则共需750元;若购进A种型号衣服2件,B种型号衣服5件,则共需680元;已知销售一件A型号衣服可获利-数学
题文
| 某商场准备进一批不同型号的衣服,若购进A种型号衣服5件,B种型号衣服3件,则共需750元;若购进A种型号衣服2件,B种型号衣服5件,则共需680元;已知销售一件A型号衣服可获利12元,销售一件B型号衣服可获利20元,要使在这次销售中获利不少于510元,且A型号衣服的数量不多于28件. (1)求A、B型号衣服进价各是多少元? (2)若购进A型号衣服的数量是B型号衣服的2倍还多4件,则商店在这次进货中可有几种方案?并简述购货方案. |