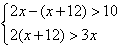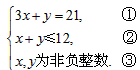某住宅小区计划购买并种植某种树苗进行绿化,在甲苗圃用4000元将树苗购买一空却仍然不够,还需2倍这种树苗,于是小区又用8200元在乙苗圃购进所需树苗,只是单价比在甲苗圃购-数学
题文
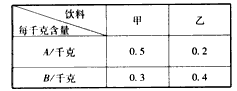
| 某住宅小区计划购买并种植某种树苗进行绿化,在甲苗圃用4000元将树苗购买一空却仍然不够,还需2倍这种树苗,于是小区又用8200元在乙苗圃购进所需树苗,只是单价比在甲苗圃购买的要贵1元. (1)这种树苗小区一共种植了多少棵? (2)小区筹备建党90周年庆祝活动,决定利用甲苗圃现有的5202盆菊花和乙苗圃现有的3195盆太阳花搭配A、B两种园艺造型,围住种植的每一棵树使其更加美丽,已知搭配一个A造型需菊花花卉12盆,太阳花花卉15盆,搭配一个B造型需菊花花卉18盆,太阳花花卉10盆. ①八年级二班课外活动小组承接了这个园艺造型搭配方案的设计,问符合题意的搭配方案有几种?请你帮助设计出来. ②若搭配一个A种造型的成本是46元,搭配一个B造型的成本是48元,试说明①中哪种方案成本最低?最低成本是多少元? |
答案
(1)设这种小树开始在甲苗圃购买了x棵.
解得,x=100, 经检验x=100是原方程的根. 所以,100+200=300. 共买树苗300棵; (2)①可设搭配A造型为y,
33≤y≤39, 搭配A造型为33棵,则搭配B造型为267棵, 搭配A造型为34棵,则搭配B造型为266棵, 搭配A造型为35棵,则搭配B造型为265棵, 搭配A造型为36棵,则搭配B造型为264棵, 搭配A造型为37棵,则搭配B造型为263棵, 搭配A造型为38棵,则搭配B造型为262棵, 搭配A造型为39棵,则搭配B造型为261棵, 所以共有7种方案. ②当A造型为39时成本最低. 39×46+(300-39)×48=14322. 最低成本为14322元. |
据专家权威分析,试题“某住宅小区计划购买并种植某种树苗进行绿化,在甲苗圃用4000元将..”主要考查你对 一元一次不等式组的应用 等考点的理解。关于这些考点的“档案”如下:
一元一次不等式组的应用
考点名称:一元一次不等式组的应用
- 应用:列一元一次不等式组解决实际问题。
一元一次不等式的应用主要涉及问题:
1.分配问题:
例:一堆玩具分给若干个小朋友,若每人分3件,则剩余4件,若前面每人分4件,则最后一人得到的玩具最多3件,问小朋友的人数至少有多少人?。
2.积分问题:
例:某次数学测验共20道题(满分100分)。评分办法是:答对1道给5分,答错1道扣2分,不答不给分。某学生有1道未答。那么他至少答对几道题才能及格?
3.比较问题:
例:某校校长暑假将带领该校“三好学生”去三峡旅游,甲旅行社说:如果校长买全票一张,则其余学生可享受半价优惠;乙旅行社说:包括校长在内全部按全票的6折优惠。已知两家旅行社的全票价都是240元,至少要多少名学生选甲旅行社比较好?4.行程问题:
例:抗洪抢险,向险段运送物资,共有120公里原路程,需要1小时送到,前半小时已经走了50公里后,后半小时速度多大才能保证及时送到?5.车费问题:
例:出租汽车起价是10元(即行驶路程在5km以内需付10元车费),达到或超过5km后,每增加1km加价1.2元(不足1km部分按1km计),现在某人乘这种出租 汽车从甲地到乙地支付车费17.2元,从甲地到乙地的路程超过多少km?
6.浓度问题:
例:在1千克含有40克食盐的海水中,在加入食盐,使他成为浓度不底于20%的食盐水,问:至少加入多少食盐?7.增减问题:
例:一根长20cm的弹簧,一端固定,另一端挂物体。在弹簧伸长后的长度不超过30cm的限度内,每挂1㎏质量的物体,弹簧伸长0.5cm.求弹簧所挂物体的最大质量是多少?8.销售问题:
例:商场购进某种商品m件,每件按进价加价30元售出全部商品的65%,然后再降价10%,这样每件仍可获利18元,又售出全部商品的25%。
(1)试求该商品的进价和第一次的售价;
(2)为了确保这批商品总的利润率不低于25%,剩余商品的售价应不低于多少元?- 一元一次不等式组解应用题的一般步骤为:
列不等式组解决实际问题的步骤与列一元一次不等式解应用题的步骤相类似,所不同的是,前者需寻求的不等关系往往不止一个,而后者只需找出一个不等关系即可。
(1)审:认真审题,分清已知量、未知量及其关系,找出题中的不等关系,要抓住题中的关键词语,如“大于”、“小于”、“不大于”、“至少”、“不超过”、“超过”等;
(2)设:设出适当的未知数;
(3)列:根据题中的不等关系列出不等式组;
(4)解:解出所列不等式组的解集;
(5)答:写出答案,从不等式组的解集中找出符合题意的答案,并检验是否符合题意。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |