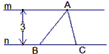
如图所示,梯形的上底长是5cm,下底长是13cm.当梯形的高由大变小时,梯形的面积也随之发生变化.(1)在这个变化过程中,自变量是______,因变量是______.(2)梯形的面积y(cm2)与-数学
题文
| 如图所示,梯形的上底长是5cm,下底长是13cm.当梯形的高由大变小时,梯形的面积也随之发生变化. (1)在这个变化过程中,自变量是______,因变量是______. (2)梯形的面积y(cm2)与高x(cm)之间的关系式为______. (3)当梯形的高由l0cm变化到1cm时,梯形的面积由______cm2变化到______cm2.  |

![变量x与y之间的关系是y=x2﹣3,当自变量x=2时,因变量y的值是[]A.﹣2B.﹣1C.1D.2-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/60/2019-03-22/975697e48a3bb17511588adca9d57c39.png)
![一长为5m,宽为2m的长方形木板,现要在长边上截去长为xm的一部分(如图),与剩余木板的面积y(m2)与x(m)的关系式为(0≤x<5)[]A.y=2xB.y=5xC.y=10﹣2xD.y=10﹣x-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/60/2019-03-22/37b269bb1c8ec823470958834f274ce5.png)
![设半径为r的圆的周长为C,则C=2πr,下列说法错误的是[]A.常量是π和2B.常量是2C.用C表示r为D.变量是C和r-八年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/60/2019-03-22/98364be396d2e14a7fe5b545e353cfd5.jpg)