如图,四边形OABC是一张放在平面直角坐标系中的正方形纸片,点O与坐标原点重合,点A在x轴上,点C在y轴上,OC=4,点E为BC的中点,点N的坐标为(3,0),过点N且平行于y轴的直线-九年级数学
题文
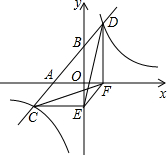
| 如图,四边形OABC是一张放在平面直角坐标系中的正方形纸片,点O与坐标原点重合,点A在x轴上,点C在y轴上,OC=4,点E为BC的中点,点N的坐标为(3,0),过点N且平行于y轴的直线MN与EB交于点M,现将纸片折叠,使顶点C落在MN上,并与MN上的点G重合,折痕为EF,点F为折痕与y轴的交点。 |
|
|
| (1)求点G的坐标; (2)求折痕EF所在直线的解析式; (3)设点P为直线EF上的点,是否存在这样的点P,使得以P,F,G为顶点的三角形为等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由。 |
答案
解:(1)∵四边形 是正方形 是正方形∴  ∵E为CB中点 ∴  ∵  轴, 轴, ∴  且 且 ∴  而  ∴  ∴  ∴  ∴  。 。(2)∵  ∴  ∴  ∴  ∴  设直线EF的解析式:  ∴  ∴  ∴折痕EF所在直线解析式:  。 。(3)  , , 。 。 |
据专家权威分析,试题“如图,四边形OABC是一张放在平面直角坐标系中的正方形纸片,点O与..”主要考查你对 求一次函数的解析式及一次函数的应用,等腰三角形的性质,等腰三角形的判定,解直角三角形 等考点的理解。关于这些考点的“档案”如下:
求一次函数的解析式及一次函数的应用等腰三角形的性质,等腰三角形的判定解直角三角形
考点名称:求一次函数的解析式及一次函数的应用
- 待定系数法求一次函数的解析式:
先设出函数解析式,再根据条件确定解析式中的未知系数,从而得到函数的解析式的方法。
一次函数的应用:
应用一次函数解应用题,一般是先写出函数解析式,在依照题意,设法求解。
(1)有图像的,注意坐标轴表示的实际意义及单位;
(2)注意自变量的取值范围。 用待定系数法求一次函数解析式的四个步骤:
第一步(设):设出函数的一般形式。(称一次函数通式)
第二步(代):代入解析式得出方程或方程组。
第三步(求):通过列方程或方程组求出待定系数k,b的值。
第四步(写):写出该函数的解析式。
一次函数的应用涉及问题:
一、分段函数问题
分段函数是在不同区间有不同对应方式的函数,要特别注意自变量取值范围的划分,既要科学合理,又要符
合实际。二、函数的多变量问题
解决含有多变量问题时,可以分析这些变量的关系,选取其中一个变量作为自变量,然后根据问题的条件寻
求可以反映实际问题的函数三、概括整合
(1)简单的一次函数问题:①建立函数模型的方法;②分段函数思想的应用。
(2)理清题意是采用分段函数解决问题的关键。
生活中的应用:
1.当时间t一定,距离s是速度v的一次函数。s=vt。
2.如果水池抽水速度f一定,水池里水量g是抽水时间t的一次函数。设水池中原有水量S。g=S-ft。
3.当弹簧原长度b(未挂重物时的长度)一定时,弹簧挂重物后的长度y是重物重量x的一次函数,即y=kx+b(k为任意正数)一次函数应用常用公式:
1.求函数图像的k值:(y1-y2)/(x1-x2)
2.求与x轴平行线段的中点:(x1+x2)/2
3.求与y轴平行线段的中点:(y1+y2)/2
4.求任意线段的长:√[(x1-x2)2+(y1-y2)2 ]
5.求两个一次函数式图像交点坐标:解两函数式
两个一次函数 y1=k1x+b1; y2=k2x+b2 令y1=y2 得k1x+b1=k2x+b2 将解得的x=x0值代回y1=k1x+b1 ; y2=k2x+b2 两式任一式 得到y=y0 则(x0,y0)即为 y1=k1x+b1 与 y2=k2x+b2 交点坐标
6.求任意2点所连线段的中点坐标:[(x1+x2)/2,(y1+y2)/2]
7.求任意2点的连线的一次函数解析式:(x-x1)/(x1-x2)=(y-y1)/(y1-y2) (若分母为0,则分子为0)
(x,y)为 + ,+(正,正)时该点在第一象限
(x,y)为 - ,+(负,正)时该点在第二象限
(x,y)为 - ,-(负,负)时该点在第三象限
(x,y)为 + ,-(正,负)时该点在第四象限
8.若两条直线y1=k1x+b1//y2=k2x+b2,则k1=k2,b1≠b2
9.如两条直线y1=k1x+b1⊥y2=k2x+b2,则k1×k2=-1
10.
y=k(x-n)+b就是直线向右平移n个单位
y=k(x+n)+b就是直线向左平移n个单位
y=kx+b+n就是向上平移n个单位
y=kx+b-n就是向下平移n个单位
口决:左加右减相对于x,上加下减相对于b。
11.直线y=kx+b与x轴的交点:(-b/k,0) 与y轴的交点:(0,b)
考点名称:等腰三角形的性质,等腰三角形的判定
- 定义:
有两条边相等的三角形,是等腰三角形,相等的两条边叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角。 等腰三角形的性质:
1.等腰三角形的两个底角度数相等(简写成“等边对等角”)。
2.等腰三角形的顶角的平分线,底边上的中线,底边上的高重合(简写成“等腰三角形的三线合一”)。
3.等腰三角形的两底角的平分线相等(两条腰上的中线相等,两条腰上的高相等)。
4.等腰三角形底边上的垂直平分线到两条腰的距离相等。
5.等腰三角形的一腰上的高与底边的夹角等于顶角的一半。
6.等腰三角形底边上任意一点到两腰距离之和等于一腰上的高(需用等面积法证明)。
7.等腰三角形是轴对称图形,只有一条对称轴,顶角平分线所在的直线是它的对称轴,等边三角形有三条对称轴。
8.等腰三角形中腰的平方等于高的平方加底的一半的平方
9.等腰三角形中腰大于高
10.等腰三角形底边延长线上任意一点到两腰距离之差等于一腰上的高(需用等面积法证明)等腰三角形的判定:
1.定义法:在同一三角形中,有两条边相等的三角形是等腰三角形。
2.判定定理:在同一三角形中,有两个角相等的三角形是等腰三角形(简称:等角对等边)。
3.顶角的平分线,底边上的中分线,底边上的高的重合的三角形是等腰三角形。
考点名称:解直角三角形
- 概念:
在直角三角形中,除直角外,一共有五个元素,即三条边和两个锐角,由直角三角形中除直角外的已知元素,求出所有未知元素的过程叫做解直角三角形。
解直角三角形的边角关系:
在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,
(1)三边之间的关系: (勾股定理);
(勾股定理);
(2)锐角之间的关系:∠A+∠B=90°;
(3)边角之间的关系: 。
。 解直角三角形的函数值:

锐角三角函数:
sinA=a/c,cosA=b/c,tanA=a/b,cotA=b/a
(1)互余角的三角函数值之间的关系:
若∠ A+∠ B=90°,那么sinA=cosB或sinB=cosA
(2)同角的三角函数值之间的关系:
①sin2A+cos2A=1
②tanA=sinA/cosA
③tanA=1/tanB
④a/sinA=b/sinB=c/sinC
(3)锐角三角函数随角度的变化规律:
锐角∠A的tan值和sin值随着角度的增大而增大,cos值随着角度的增大而减小。- 解直角三角形的应用:
一般步骤是:
(1)将实际问题抽象为数学问题(画图,转化为直角三角形的问题);
(2)根据题目的条件,适当选择锐角三角函数等去解三角形;
(3)得到数学问题的答案;
(4)还原为实际问题的答案。 解直角三角形的函数值列举:
sin1=0.01745240643728351 sin2=0.03489949670250097 sin3=0.05233595624294383
sin4=0.0697564737441253 sin5=0.08715574274765816 sin6=0.10452846326765346
sin7=0.12186934340514747 sin8=0.13917310096006544 sin9=0.15643446504023087
sin10=0.17364817766693033 sin11=0.1908089953765448 sin12=0.20791169081775931
sin13=0.22495105434386497 sin14=0.24192189559966773 sin15=0.25881904510252074
sin16=0.27563735581699916 sin17=0.2923717047227367 sin18=0.3090169943749474
sin19=0.3255681544571567 sin20=0.3420201433256687 sin21=0.35836794954530027
sin22=0.374606593415912 sin23=0.3907311284892737 sin24=0.40673664307580015
sin25=0.42261826174069944 sin26=0.4383711467890774 sin27=0.45399049973954675
sin28=0.4694715627858908 sin29=0.48480962024633706 sin30=0.49999999999999994
sin31=0.5150380749100542 sin32=0.5299192642332049 sin33=0.544639035015027
sin34=0.5591929034707468 sin35=0.573576436351046 sin36=0.5877852522924731
sin37=0.6018150231520483 sin38=0.6156614753256583 sin39=0.6293203910498375
sin40=0.6427876096865392 sin41=0.6560590289905073 sin42=0.6691306063588582
sin43=0.6819983600624985 sin44=0.6946583704589972 sin45=0.7071067811865475
sin46=0.7193398003386511 sin47=0.7313537016191705 sin48=0.7431448254773941
sin49=0.7547095802227719 sin50=0.766044443118978 sin51=0.7771459614569708
sin52=0.7880107536067219 sin53=0.7986355100472928 sin54=0.8090169943749474
sin55=0.8191520442889918 sin56=0.8290375725550417 sin57=0.8386705679454239
sin58=0.848048096156426 sin59=0.8571673007021122 sin60=0.8660254037844386
sin61=0.8746197071393957 sin62=0.8829475928589269 sin63=0.8910065241883678
sin64=0.898794046299167 sin65=0.9063077870366499 sin66=0.9135454576426009
sin67=0.9205048534524404 sin68=0.9271838545667873 sin69=0.9335804264972017
sin70=0.9396926207859083 sin71=0.9455185755993167 sin72=0.9510565162951535
sin73=0.9563047559630354 sin74=0.9612616959383189 sin75=0.9659258262890683
sin76=0.9702957262759965 sin77=0.9743700647852352 sin78=0.9781476007338057
sin79=0.981627183447664 sin80=0.984807753012208 sin81=0.9876883405951378
sin82=0.9902680687415704 sin83=0.992546151641322 sin84=0.9945218953682733
sin85=0.9961946980917455 sin86=0.9975640502598242 sin87=0.9986295347545738
sin88=0.9993908270190958 sin89=0.9998476951563913
sin90=1cos1=0.9998476951563913 cos2=0.9993908270190958 cos3=0.9986295347545738
cos4=0.9975640502598242 cos5=0.9961946980917455 cos6=0.9945218953682733
cos7=0.992546151641322 cos8=0.9902680687415704 cos9=0.9876883405951378
cos10=0.984807753012208 cos11=0.981627183447664 cos12=0.9781476007338057
cos13=0.9743700647852352 cos14=0.9702957262759965 cos15=0.9659258262890683
cos16=0.9612616959383189 cos17=0.9563047559630355 cos18=0.9510565162951535
cos19=0.9455185755993168 cos20=0.9396926207859084 cos21=0.9335804264972017
cos22=0.9271838545667874 cos23=0.9205048534524404 cos24=0.9135454576426009
cos25=0.9063077870366499 cos26=0.898794046299167 cos27=0.8910065241883679
cos28=0.882947592858927 cos29=0.8746197071393957 cos30=0.8660254037844387
cos31=0.8571673007021123 cos32=0.848048096156426 cos33=0.838670567945424
cos34=0.8290375725550417 cos35=0.8191520442889918 cos36=0.8090169943749474
cos37=0.7986355100472928 cos38=0.7880107536067219 cos39=0.7771459614569709
cos40=0.766044443118978 cos41=0.754709580222772 cos42=0.7431448254773942
cos43=0.7313537016191705 cos44=0.7193398003386512 cos45=0.7071067811865476
cos46=0.6946583704589974 cos47=0.6819983600624985 cos48=0.6691306063588582
cos49=0.6560590289905074 cos50=0.6427876096865394 cos51=0.6293203910498375
cos52=0.6156614753256583 cos53=0.6018150231520484 cos54=0.5877852522924731
cos55=0.5735764363510462 cos56=0.5591929034707468 cos57=0.5446390350150272
cos58=0.5299192642332049 cos59=0.5150380749100544 cos60=0.5000000000000001
cos61=0.4848096202463371 cos62=0.46947156278589086 cos63=0.4539904997395468
cos64=0.43837114678907746 cos65=0.42261826174069944 cos66=0.4067366430758004
cos67=0.3907311284892737 cos68=0.3746065934159122 cos69=0.35836794954530015
cos70=0.3420201433256688 cos71=0.32556815445715675 cos72=0.30901699437494745
cos73=0.29237170472273677 cos74=0.27563735581699916 cos75=0.25881904510252074
cos76=0.24192189559966767 cos77=0.22495105434386514 cos78=0.20791169081775923
cos79=0.19080899537654491 cos80=0.17364817766693041 cos81=0.15643446504023092
cos82=0.13917310096006546 cos83=0.12186934340514749 cos84=0.10452846326765346
cos85=0.08715574274765836 cos86=0.06975647374412523 cos87=0.052335956242943966
cos88=0.03489949670250108 cos89=0.0174524064372836
cos90=0tan1=0.017455064928217585 tan2=0.03492076949174773 tan3=0.052407779283041196
tan4=0.06992681194351041 tan5=0.08748866352592401 tan6=0.10510423526567646
tan7=0.1227845609029046 tan8=0.14054083470239145 tan9=0.15838444032453627
tan10=0.17632698070846497 tan11=0.19438030913771848 tan12=0.2125565616700221
tan13=0.2308681911255631 tan14=0.24932800284318068 tan15=0.2679491924311227
tan16=0.2867453857588079 tan17=0.30573068145866033 tan18=0.3249196962329063
tan19=0.34432761328966527 tan20=0.36397023426620234 tan21=0.3838640350354158
tan22=0.4040262258351568 tan23=0.4244748162096047 tan24=0.4452286853085361
tan25=0.4663076581549986 tan26=0.4877325885658614 tan27=0.5095254494944288
tan28=0.5317094316614788 tan29=0.554309051452769 tan30=0.5773502691896257
tan31=0.6008606190275604 tan32=0.6248693519093275 tan33=0.6494075931975104
tan34=0.6745085168424265 tan35=0.7002075382097097 tan36=0.7265425280053609
tan37=0.7535540501027942 tan38=0.7812856265067174 tan39=0.8097840331950072
tan40=0.8390996311772799 tan41=0.8692867378162267 tan42=0.9004040442978399
tan43=0.9325150861376618 tan44=0.9656887748070739 tan45=0.9999999999999999
tan46=1.0355303137905693 tan47=1.0723687100246826 tan48=1.1106125148291927
tan49=1.1503684072210092 tan50=1.19175359259421 tan51=1.234897156535051
tan52=1.2799416321930785 tan53=1.3270448216204098 tan54=1.3763819204711733
tan55=1.4281480067421144 tan56=1.4825609685127403 tan57=1.5398649638145827
tan58=1.6003345290410506 tan59=1.6642794823505173 tan60=1.7320508075688767
tan61=1.8040477552714235 tan62=1.8807264653463318 tan63=1.9626105055051503
tan64=2.050303841579296 tan65=2.1445069205095586 tan66=2.246036773904215
tan67=2.355852365823753 tan68=2.4750868534162946 tan69=2.6050890646938023
tan70=2.7474774194546216 tan71=2.904210877675822 tan72=3.0776835371752526
tan73=3.2708526184841404 tan74=3.4874144438409087 tan75=3.7320508075688776
tan76=4.0107809335358455 tan77=4.331475874284153 tan78=4.704630109478456
tan79=5.144554015970307 tan80=5.671281819617707 tan81=6.313751514675041
tan82=7.115369722384207 tan83=8.144346427974593 tan84=9.514364454222587
tan85=11.43005230276132 tan86=14.300666256711942 tan87=19.08113668772816
tan88=28.636253282915515 tan89=57.289961630759144
tan90=(无限)
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |