已知A(﹣1,0),B(0,﹣3),点C与点A关于坐标原点对称,经过点C的直线与y轴交于点D,与直线AB交于点E,且E点在第二象限.(1)求直线AB的解析式;(2)若点D(0,1),过点B作BF⊥CD于-八年级数学
题文
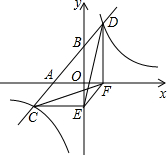
| 已知A(﹣1,0),B(0,﹣3),点C与点A关于坐标原点对称,经过点C的直线与y轴交于点D,与直线AB交于点E,且E点在第二象限. (1)求直线AB的解析式; (2)若点D(0,1),过点B作BF⊥CD于F,连接BC,求∠DBF的度数及△BCE的面积; (3)若点G(G不与C重合)是动直线CD上一点,且BG=BA,试探究∠ABG与∠ACE之间满足的等量关系,并加以证明. |
答案
| 解:(1)依题意,设直线AB的解析式为 y=kx﹣3 ∵A(﹣1,0)在直线上, ∴0=﹣k﹣3. ∴k=﹣3. ∴直线AB的解析式为y=﹣3x﹣3. (2)如图1,依题意,C(1,0),OC=1.由D(0,1),得OD=1. 在△DOC中,∠DOC=90°,OD=OC=1.可得∠CDO=45°. ∵BF⊥CD于F, ∴∠BFD=90°. ∴∠DBF=90°﹣∠CDO=45°. 可求得直线CD的解析式为y=﹣x+1 由  解得 解得  ∴直线AB与CD的交点为E(﹣2,3). 过E作EH⊥y轴于H,则EH=2. ∵B(0,﹣3),D(0,1), ∴BD=4. ∴S△BCE=S△BDE+S△BDC=  ×4×2+ ×4×2+  ×4×1=6 ×4×1=6(3)连接BC,作BM⊥CD于M. ∵AO=OC,BO⊥AC, ∴BA=BC. ∴∠ABO=∠CBO. 设∠CBO=α,则∠ABO=α,∠ACB=90°﹣α. ∵BG=BA, ∴BG=BC. ∵BM⊥CD, ∴∠CBM=∠GBM. 设∠CBM=β,则∠GBM=β,∠BCG=90°﹣β. (i) 如图2,当点G在射线CD的反向延长线上时, ∵∠ABG=2α+2β=2(α+β) ∠ECA=180°﹣(90°﹣α)﹣(90°﹣β)=α+β ∴∠ABG=2∠ECA. (ii) 如图3,当点G在射线CD的延长线上时, ∵∠ABG=2α﹣2β=2(α﹣β) ∠ECA=(90°﹣β)﹣(90°﹣α)=α﹣β ∴∠ABG=2∠ECA. 综上,∠ABG=2∠ECA. |
   |
据专家权威分析,试题“已知A(﹣1,0),B(0,﹣3),点C与点A关于坐标原点对称,经过点C的直..”主要考查你对 求一次函数的解析式及一次函数的应用,角的概念 等考点的理解。关于这些考点的“档案”如下:
求一次函数的解析式及一次函数的应用角的概念
考点名称:求一次函数的解析式及一次函数的应用
- 待定系数法求一次函数的解析式:
先设出函数解析式,再根据条件确定解析式中的未知系数,从而得到函数的解析式的方法。
一次函数的应用:
应用一次函数解应用题,一般是先写出函数解析式,在依照题意,设法求解。
(1)有图像的,注意坐标轴表示的实际意义及单位;
(2)注意自变量的取值范围。 用待定系数法求一次函数解析式的四个步骤:
第一步(设):设出函数的一般形式。(称一次函数通式)
第二步(代):代入解析式得出方程或方程组。
第三步(求):通过列方程或方程组求出待定系数k,b的值。
第四步(写):写出该函数的解析式。
一次函数的应用涉及问题:
一、分段函数问题
分段函数是在不同区间有不同对应方式的函数,要特别注意自变量取值范围的划分,既要科学合理,又要符
合实际。二、函数的多变量问题
解决含有多变量问题时,可以分析这些变量的关系,选取其中一个变量作为自变量,然后根据问题的条件寻
求可以反映实际问题的函数三、概括整合
(1)简单的一次函数问题:①建立函数模型的方法;②分段函数思想的应用。
(2)理清题意是采用分段函数解决问题的关键。
生活中的应用:
1.当时间t一定,距离s是速度v的一次函数。s=vt。
2.如果水池抽水速度f一定,水池里水量g是抽水时间t的一次函数。设水池中原有水量S。g=S-ft。
3.当弹簧原长度b(未挂重物时的长度)一定时,弹簧挂重物后的长度y是重物重量x的一次函数,即y=kx+b(k为任意正数)一次函数应用常用公式:
1.求函数图像的k值:(y1-y2)/(x1-x2)
2.求与x轴平行线段的中点:(x1+x2)/2
3.求与y轴平行线段的中点:(y1+y2)/2
4.求任意线段的长:√[(x1-x2)2+(y1-y2)2 ]
5.求两个一次函数式图像交点坐标:解两函数式
两个一次函数 y1=k1x+b1; y2=k2x+b2 令y1=y2 得k1x+b1=k2x+b2 将解得的x=x0值代回y1=k1x+b1 ; y2=k2x+b2 两式任一式 得到y=y0 则(x0,y0)即为 y1=k1x+b1 与 y2=k2x+b2 交点坐标
6.求任意2点所连线段的中点坐标:[(x1+x2)/2,(y1+y2)/2]
7.求任意2点的连线的一次函数解析式:(x-x1)/(x1-x2)=(y-y1)/(y1-y2) (若分母为0,则分子为0)
(x,y)为 + ,+(正,正)时该点在第一象限
(x,y)为 - ,+(负,正)时该点在第二象限
(x,y)为 - ,-(负,负)时该点在第三象限
(x,y)为 + ,-(正,负)时该点在第四象限
8.若两条直线y1=k1x+b1//y2=k2x+b2,则k1=k2,b1≠b2
9.如两条直线y1=k1x+b1⊥y2=k2x+b2,则k1×k2=-1
10.
y=k(x-n)+b就是直线向右平移n个单位
y=k(x+n)+b就是直线向左平移n个单位
y=kx+b+n就是向上平移n个单位
y=kx+b-n就是向下平移n个单位
口决:左加右减相对于x,上加下减相对于b。
11.直线y=kx+b与x轴的交点:(-b/k,0) 与y轴的交点:(0,b)
考点名称:角的概念
角的基本概念:
从静态角度认识角:由一个点出发的两条射线组成的图形叫角;
从动态角度认识角:一条射线绕着它的顶点旋转到另一个位置,则这两条射线组成的图像叫角。有公共端点的两条射线组成的图形叫做角,这个公共端点叫做角的顶点,这两条射线叫做角的边。
①因为射线是向一方无限延伸的,所以角的两边无所谓长短,即角的大小与它的边长无关。
②角的大小可以度量,可以比较。
③根据角的度数,角可以分为锐角、直角、钝角、平角、周角。
角的表示:角可以用大写英文字母、阿拉伯数字或小写的希腊字母表示,如∠1,∠α,∠BAD等。- 角的分类:
根据角的度数,角可以分为锐角、直角、钝角、平角、周角。
平角:180。的角,当角的两边在一条直线上时,组成的角叫做平角。即射线OA绕点O旋转,当终边在始边OA的反向延长线上时所成的角;
直角:90。的角,即线OA绕点O旋转,当终边与始边垂直时所成的角,平角的一半叫做直角;
锐角:大于0。小于90。的角,小于直角的角叫做锐角;
钝角:大于90。小于180。的角,大于直角且小于平角的角叫做钝角。
周角:360。的角,即射线OA绕点O旋转,当终边与始边重合时所成的角。
角的性质:
①角的大小与边的长短无关,只与构成角的两条射线的幅度大小有关;
②角的大小可以度量,可以比较;
③角可以参与运算。
角的度量:
角的度量有如下规定:把一个平角180等分,每一份就是1度的角,单位是度,用“。”,1度记作“1°”,n度记作“n°”。把1°的角60等分,每一份叫做1分的角,1分记作“1′”。把1′的角60等分,每一份叫做1秒的角,1秒记作“1″”。1°=60′=3600″。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |