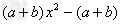若xy=35,则2x-yy=______,分解因式:a2b-2ab+b=______.-数学
题文
若
|
答案
∵
∴x=
∴
a2b-2ab+b=b(a2-2a+1)=b(a-1)2, 故答案为:
|
据专家权威分析,试题“若xy=35,则2x-yy=______,分解因式:a2b-2ab+b=______.-数学-魔方..”主要考查你对 因式分解,比例的性质 等考点的理解。关于这些考点的“档案”如下:
因式分解比例的性质
考点名称:因式分解
- 定义:把一个多项式化为几个整式的积的形式,这种变形叫做把这个多项式因式分解,也叫作把这个多项式分解因式。
它是中学数学中最重要的恒等变形之一,它被广泛地应用于初等数学之中,是我们解决许多数学问题的有力工具。 - 因式分解没有普遍适用的方法,初中数学教材中主要介绍了提公因式法、运用公式法、分组分解法。而在竞赛上,又有拆项和添减项法,十字相乘法,待定系数法,双十字相乘法,对称多项式,轮换对称多项式法,余式定理法,求根公式法,换元法,长除法,短除法,除法等。
注意四原则:
1.分解要彻底(是否有公因式,是否可用公式)
2.最后结果只有小括号
3.最后结果中多项式首项系数为正(例如:)不一定首项一定为正。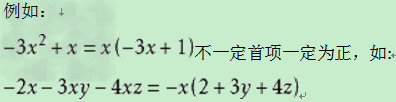
因式分解中的四个注意:
①首项有负常提负,
②各项有“公”先提“公”,
③某项提出莫漏1,
④括号里面分到“底”。
现举下例,可供参考。
例:
把-a2-b2+2ab+4分解因式。
解:-a2-b2+2ab+4
=-(a2-2ab+b2-4)
=-[(a-b)2-4]
=-(a-b+2)(a-b-2)
这里的“负”,指“负号”。
如果多项式的第一项是负的,一般要提出负号,使括号内第一项系数是正的;这里的“公”指“公因式”。
如果多项式的各项含有公因式,那么先提取这个公因式,再进一步分解因式;这里的“1”,是指多项式的某个整项是公因式时,先提出这个公因式后,括号内切勿漏掉1。
分解因式,必须进行到每一个多项式因式都不能再分解为止。即分解到底,不能半途而废的意思。
其中包含提公因式要一次性提“干净”,不留“尾巴”,并使每一个括号内的多项式都不能再分解。
在没有说明化到实数时,一般只化到有理数就够了,有说明实数的话,一般就要化到实数!
由此看来,因式分解中的四个注意贯穿于因式分解的四种基本方法之中,与因式分解的四个步骤或说一般思考顺序的四句话:“先看有无公因式,再看能否套公式,十字相乘试一试,分组分解要合适”等是一脉相承的。分解步骤:
①如果多项式的各项有公因式,那么先提公因式;
②如果各项没有公因式,那么可尝试运用公式、十字相乘法来分解;
③如果用上述方法不能分解,那么可以尝试用分组、拆项、补项法来分解
④分解因式,必须进行到每一个多项式因式都不能再分解为止。
也可以用一句话来概括:“先看有无公因式,再看能否套公式。十字相乘试一试,分组分解要相对合适。”分解因式技巧掌握:
①分解因式是多项式的恒等变形,要求等式左边必须是多项式
②分解因式的结果必须是以乘积的形式表示
③每个因式必须是整式,且每个因式的次数都必须低于原来多项式的次数
④分解因式必须分解到每个多项式因式都不能再分解为止。
注:分解因式前先要找到公因式,在确定公因式前,应从系数和因式两个方面考虑。主要方法:
1.提取公因式法:
如果一个多项式的各项有公因式,可以把这个公因式提出来,从而将多项式化成两个因式乘积的形式,这种分解因式的方法叫做提公因式法。
提公因式法基本步骤:
(1)找出公因式
(2)提公因式并确定另一个因式:
①第一步找公因式可按照确定公因式的方法先确定系数再确定字母
②第二步提公因式并确定另一个因式,注意要确定另一个因式,可用原多项式除以公因式,所得的商即是提公因式后剩下的一个因式,也可用公因式分别除去原多项式的每一项,求的剩下的另一个因式
③提完公因式后,另一因式的项数与原多项式的项数相同。
2.公式法:
把乘法公式的平方差公式和完全平方公式反过来,得到因式分解的公式:
平方差公式:a2-b2=(a+b)·(a-b);
完全平方式:a2±2ab+b2=(a±b)2;
立方差公式: 。
。
3.分组分解法:
利用分组分解因式的方法叫做分组分解法,ac+ad+bc+bd=a·(c+d)+b·(c+d)=(a+b)·(c+d)
其原则:
①连续提取公因式法:分组后每组能够分解因式,每组分解因式后,组与组之间又有公因式可提。
②分组后直接运用公式法:分组后各组内可以直接应用公式,各组分解因式后,使组与组之间构成公式的形式,然后用公式法分解因式。
4.十字相乘法:a2+(p+q)·a+p·q=(a+p)·(a+q)。
5.解方程法:
通过解方程来进行因式分解,如
x2+2x+1=0 ,解,得x1=-1,x2=-1,就得到原式=(x+1)×(x+1)
6.待定系数法:
首先判断出分解因式的形式,然后设出相应整式的字母系数,求出字母系数,从而把多项式因式分解。
例:
分解因式x -x -5x -6x-4
分析:易知这个多项式没有一次因式,因而只能分解为两个二次因式。
解:
设x -x -5x -6x-4
=(x +ax+b)(x +cx+d)
= x +(a+c)x +(ac+b+d)x +(ad+bc)x+bd
所以 解得 a=1,b=1,c=-2,d=-4
则x -x -5x -6x-4 =(x +x+1)(x -2x-4)
考点名称:比例的性质
- 比例:
在数学中,比例是一个总体中各个部分的数量占总体数量的比重,用于反映总体的构成或者结构。两种相关联的量,一种量变化,另一种量也随着变化。要想判断两个比式子能不能组成比例,要看它们的比例是不是相等。
比例性质:
比例的基本性质:组成比例的四个数,叫做比例的项。两端的两项叫做比例的外项,中间的两项叫做比例的内项。
在比例里,两个外项的积等于两个内项的积。 ,则有
,则有 。
。
证明:


2.分比性质:
在一个比例等式中,第一个比例的前后项之差与第一个比例的后项的比,等于第二个比例的前后项之差与第二个比例的后项的比。
例:已知a,b,c,d∈C,且有b≠0,d≠0,如果 ,则有
,则有 。
。
证明:


3.合分比性质:
在一个比例等式中,第一个比例的前后项之和与第一个比例的前后项之差的比,等于第二个比例的前后项之和与第二个比例的前后项之差的比。
例:已知a,b,c,d∈C,且有b≠0,d≠0,如果 ,则有
,则有 。
。
证明:
令 ,则
,则 ,
,


4.等比性质:
在一个比例等式中,两前项之和与两后项之和的比例与原比例相等。
例:已知a,b,c,d∈C,且有b≠0,d≠0,如果 ,则有
,则有 。
。
证明:
令 ,则
,则


- 重要定理:

比例尺:
是表示图上距离比实地距离缩小的程度,因此也叫缩尺。
用公式表示为:比例尺=图上距离/实地距离。
1.数字式,用数字的比例式或分数式表示比例尺的大小。
例如地图上1厘米代表实地距离500千米,可写成:1∶50,000,000或写成:1/50,000,000。
2.线段式,在地图上画一条线段,并注明地图上1厘米所代表的实际距离。
3.文字式,在地图上用文字直接写出地图上1厘米代表实地距离多少千米,
如:图上1厘米相当于地面距离500千米,或五千万分之一。
比例线段:
1.两条线段的长度比叫做这两条线段的比。
2.在同一单位下,四条线段长度为a、b、c、d,其关系为a∶b=c∶d,那么,这四条线段叫做成比例线段,简称比例线段。
3.一般的,如果三个数a,b,c满足比例式a∶b=b∶c,则b就叫做a,c的比例中项。 - 比例的美术术语:
比例通常指物体之间形的大小、宽窄、高低的关系;另外比例也会在构图中用到,例如你在画一幅素描静物就要注意所有静物占用画面的大小关系。
在画素描的过程中要想把形画准就要注意比例了。
把握比例的几个技巧:
1.横着比:当你要画某一个物体的位置时就以此做一条贯穿整个画面的横线,看到所有在这条线上的物体。
2.竖着比:做一条贯穿画面的垂线,注意观察所有在这条线上的物体。
3.多看物体、少看画面:为的是形成观察的意识,抛弃大脑中的原始概念。看物体5秒,看画面2秒,眼睛要在画面和物体之间反复的观察比较。
4.总的说就是放长线、看整体、多比较。把这些想象成经线纬线一样会比较简单;初学者要多画辅助线,等功底深厚了你会发现你画面中的辅助线会越来越少,而你心里假象的辅助线会越来越多。
在构图中要注意的比例关系技巧:一般被画物占画面百分之八十左右,看上去饱满。
人物相关比例:
1.三庭五眼:发际线-鼻底-下巴为三庭,这三段之间每段的距离大约相等;耳根-外眼角-内眼角-内眼角-外眼角-耳根为五眼,它们之间距离大约相等。
2.站七坐五蹲三半:一个站着的成年人身高大约等于他七个头长(站七),当他座上时就等于五个头长(坐五),蹲着时刚好是三个半头长(三头)。
3.小孩的头部比例较大,站着时一般为三到四个头高。
4.张开双臂,两个中指之间的长度大约等于这个人的身高。
5.手臂的长度为两个头长(腋窝-胳膊肘-手腕各位为一个头长)。
6.手掌为三分之二头长。
7.当举起胳膊时胳膊肘刚好到头顶。
8.肩宽为两个头宽。
9.脚掌为一个头长。
10.男人肩比胯宽,而女人跨比肩宽。
还有很多,可以在生活中多总结,多观察。这些都是标准人体比例,可以帮助初学者入门;
也是艺术家创作英雄楷模人物绘画雕塑等艺术作品时的指导,例如米开朗基罗的大卫是七个半头高。在现实生活中有形形色色的人,在进行人物素描时就应当个别观察,抓住特征。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |

![下列因式分解中,完全正确的是[]A.x3-x=x(x2-1)B.x4-4=(x2+2)(x+)(x-)C.x2+4xy+4y2=(x+4y)2D.x2-y2=(x-y)2-八年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/74/2019-04-04/a63c6395e51135d0bc65ff9123292247.gif)
![下列因式分解中,结果正确的是[]A.x2﹣4=(x+2)(x﹣2)B.1﹣(x+2)2=(x+1)(x+3)C.2m2n﹣8n3=2n(m2﹣4n2)D.-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/74/2019-04-04/59c7ed12814fe600167c1fba347f028f.png)