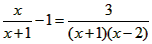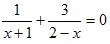把一根周长为4m的铁丝弯成一个矩形框,使它的宽与长的比为黄金比5-12.求这个矩形的面积.-数学
题文
把一根周长为4m的铁丝弯成一个矩形框,使它的宽与长的比为黄金比
|
答案
| 设这个矩形的长为xm,宽为ym,则x+y=2, 由题设得:
解得:x=
所以这个黄金矩形的面积为:(
|
据专家权威分析,试题“把一根周长为4m的铁丝弯成一个矩形框,使它的宽与长的比为黄金比..”主要考查你对 解分式方程,黄金分割数 等考点的理解。关于这些考点的“档案”如下:
解分式方程黄金分割数
考点名称:解分式方程
- 解法:
解分式方程的基本思想是把分式方程转化为整式方程,其一般步骤是:
(1)去分母:分式方程两边同乘以方程中各分母的最简公分母,把分式方程转化为整式方程。
(最简公分母:①系数取最小公倍数②出现的字母取最高次幂③出现的因式取最高次幂)
(2)解方程:解整式方程,得到方程的根;
(3)验根:将整式方程的解带入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;
否则,这个解不是原分式方程的解,是原分式方程的增根。
如果分式本身约分了,也要带进去检验。
在列分式方程解应用题时,不仅要检验所得解的是否满足方程式,还要检验是否符合题意。
一般的,解分式方程时,去分母后所得整式方程的解有可能使原方程中分母为零,因此要将整式方程的解代入最简公分母,如果最简公分母的值不为零,则是方程的解.
注意:
(1)注意去分母时,不要漏乘整式项。
(2)増根是分式方程去分母后化成的整式方程的根,但不是原分式方程的根。
(3)増根使最简公分母等于0。
分式方程的特殊解法:
换元法:
换元法是中学数学中的一个重要的数学思想,其应用非常广泛,当分式方程具有某种特殊形式,一般的去分母不易解决时,可考虑用换元法。 解分式方程的基本思路是将分式方程化为整式方程,具体做法是“去分母”,即方程两边同乘最简公分母,这也是解分式方程的一般思路和做法。
解分式方程注意:
①解分式方程的基本思想是把分式方程转化为整式方程,通过解整式方程进一步求得分式方程的解;
②用分式方程中的最简公分母同乘方程的两边,从而约去分母,但要注意用最简公分母乘方程两边各项时,切勿漏项;
③解分式方程可能产生使分式方程无意义的情况,那么检验就是解分式方程的必要步骤。
考点名称:黄金分割数
- 黄金分割数:
把一条线段分割为两部分,使其中一部分与全长之比等于另一部分与这部分之比。其比值是一个无理数,取其前三位数字的近似值是0.618。由于按此比例设计的造型十分美丽,因此称为黄金分割,也称为中外比。 - 黄金分割:
黄金分割又称黄金律,是指事物各部分间一定的数学比例关系,即将整体一分为二,较大部分与较小部分之比等于整体与较大部分之比,其比值约为1∶0.618或1.618∶1,即长段为全段的0.618。0.618被公认为最具有审美意义的比例数字。上述比例是最能引起人的美感的比例,因此被称为黄金分割。
黄金分割线:
黄金分割线是一种古老的数学方法。黄金分割的创始人是古希腊的毕达哥拉斯,他在当时十分有限的科学条件下大胆断言:
一条线段的某一部分与另一部分之比,如果正好等于另一部分同整个线段的比即0.618,那么,这样比例会给人一种美感。
后来,这一神奇的比例关系被古希腊著名哲学家、美学家柏拉图誉为“黄金分割律”。黄金分割线的神奇和魔力,在数学界上还没有明确定论,但它屡屡在实际中发挥着意想不到的作用。
黄金分割线的最基本公式,是将1分割为0.618和0.382,它们有如下一些特点:
(1)数列中任一数字都是由前两个数字之和构成。
(2)前一数字与后一数字之比例,趋近于一固定常数,即0.618。
(3)后一数字与前一数字之比例,趋近于1.618。
(4)1.618与0.618互为倒数,其乘积则约等于1。
(5)任一数字如与前面第二个数字相比,其值趋近于2.618;如与后面第二个数字相比,其值则趋近于0.382。
理顺下来,上列奇异数字组合除能反映黄金分割的两个基本比值0.618和0.382以外,尚存在下列两组神秘比值。
即: (1)0.191、0.382、0.5、0.618、0.809 (2)1、1.382、1.5、1.618、2、2.382、2.618
黄金分割点:
把一条线段分割为两部分,使其中一部分与全长之比等于另一部分与这部分之比。其比值是一个无理数,用分数表示为(√5-1)/2,取其前三位数字的近似值是0.618。由于按此比例设计的造型十分美丽,因此称为黄金分割,也称为中外比。这个分割点就叫做黄金分割点(goldensectionratio通常用φ表示)这是一个十分有趣的数字,我们以0.618来近似表示,通过简单的计算就可以发现:(1-0.618)/0.618=0.6一条线段上有两个黄金分割点。 无限不循环小数
a,b
a:b=(a+b):a
通常用希腊字母Ф表示这个值。
黄金分割奇妙之处,在于其比例与其倒数是一样的。例如:1.618的倒数是0.618,而1.618:1与1:0.618是一样的。
确切值为(√5-1)/2(x^2+x-1=0的一个根)
黄金分割数前面的32位为:0.6180339887 4989484820 458683436565
黄金分割三角形:
正五边形对角线连满后出现的所有三角形,都是黄金分割三角形。
黄金分割三角形有一个特殊性,所有的三角形都可以用四个与其本身全等的三角形来生成与其本身相似的三角形,但黄金分割三角形是唯一一种可以用5个而不是4个与其本身全等的三角形来生成与其本身相似的三角形的三角形。由于五角形的顶角是36度,这样也可以得出黄金分割的数值为2sin18°(即2*sin(π/10))。
将一个正五边形的所有对角线连接起来,所产生的五角星里面的所有三角形都是黄金分割三角形。
黄金矩形:
若矩形的宽与长的比等于(√5-1)/2≈0.618,那么这个矩形称为黄金矩形(又称根号矩形)。
黄金分割线:
由黄金分割点联想到“黄金分割线”,并类似地给出“黄金分割线”的定义:直线L将一个面积为S的图形分成两部分,这两部分的面积分别为S1、S2,如果S1:S=S2:S1,那么称直线L为该图形的黄金分割线。
与数列的关系:
让我们首先从一个数列开始,它的前面两个数是:1、1,后面的每个数都是它前面的两个数之和。
例如:1、1、2、3、5、8、13、21、34、55、89、144…..这个数列的名字叫做“斐波那契数列”,这些数被称为“斐波那契数”
斐波那契数列与黄金分割有什么关系呢?经研究发现,相邻两个菲波那契数的比值是随序号的增加而逐渐趋于黄金分割比的。
即f(n)/f(n+1)-→0.618…。由于斐波那契数都是整数,两个整数相除之商是有理数,所以只是逐渐逼近黄金分割比这个无理数。
但是当我们继续计算出后面更大的斐波那契数时,就会发现相邻两数之比确实是非常接近黄金分割比的。
一个很能说明问题的例子是五角星/正五边形。五角星是非常美丽的,中国的国旗上就有五颗,还有不少国家的国旗也用五角星,因为在五角星中可以找到的所有线段之间的长度关系都是符合黄金分割比的。
分数与根式:
有限段的黄金比1/X=X/(1-X),有X2=1-X,X(1+X)=1,得X=1/(1+X)。
有限式=无限式
对等式右边分母中的X又以1/(1+X)代替,可得X=1/(1+1/(1+X));
以此类推,可得无穷连分数:X=1/(1+1/(1+1/(1+1/(1+...。
对等式进行类似的代替,可得:X=√(1+√(1+√(1+√(1+...。
这样一个简洁的无穷连分式和无穷套根式给人以有序而无穷的印象,使人具有言而不喻的美感。黄金分割法在摄影中的应用:
一幅优秀的摄影作品,不仅要有深刻的主题思想和内容,同时还应具备与内容相一致的优美形式和协调的构图。初学摄影,在取景时了解和掌握黄金分割法。对于提高作品美学价值很有帮助。
黄金分割法,就是把一条直线段分成两部分,其中一部分对全部的比等于其余一部分对这一部分的比,常用2:3,3:5,5:8等近似值的比例关系迸引美术设计和摄影构图,这种比例也称黄金律。在摄影构图中,常使用的概略方法,就是在画面上横、竖各画两条与边平行、等分的直线,将画面分成9个相等的方块,称九宫图。直线和横线相交的4个点,称黄金分割点。
根据经验,将主体景物安排在黄金分割点附近,能更好地发挥主体景物在图面上的组织作用,有利于周围景物的协调和联系,容易引起美感,产生较好的视觉效果,使主体景物更加鲜明、突出。
另外,人们看图片和书刊有个习惯,就是由左向右移动,视线经过运动,往往视点落于右侧,所以在构图时把主要景物、醒目的形象安置在右边,更能收到良好的效果。
初学摄影取景,可选选用“黄金分割法”的练习构图,经过多次实践,有了自己的经验和体会以后,就可根据实际情况自己进行创作了。如果都千篇一律,生搬硬套这一种形式,也不可取,时间久了反而会束缚自己的创作思想,使拍出的照片四平八稳,缺乏变化,贫乏无味,就谈不上有什么艺术性。
用黄金分割法确定主体的位置,并没有完成构图的整个过程,还应注意安排必要的空间,考虑主体与陪体之间的呼应,充分表达主题的思想内容。同时,还要考虑影调,光线处理,色彩的表现等等。
为了提高基本功,还有很重要的一点,就是要认真学习美学知识,加强美学修养,并通过拍摄实践,不断总结,积累经验,多拍出一些有较高艺术水平的照片来。发现历史:
由于公元前6世纪古希腊的毕达哥拉斯学派研究过正五边形和正十边形的作图,因此现代数学家们推断当时毕达哥拉斯学派已经触及甚至掌握了黄金分割。
公元前4世纪,古希腊数学家欧多克索斯第一个系统研究了这一问题,并建立起比例理论。
公元前300年前后欧几里得撰写《几何原本》时吸收了欧多克索斯的研究成果,进一步系统论述了黄金分割,成为最早的有关黄金分割的论著。
中世纪后,黄金分割被披上神秘的外衣,意大利数家帕乔利称中末比为神圣比例,并专门为此著书立说。德国天文学家开普勒称黄金分割为神圣分割。
到19世纪黄金分割这一名称才逐渐通行。黄金分割数有许多有趣的性质,人类对它的实际应用也很广泛。最著名的例子是优选学中的黄金分割法或0.618法,是由美国数学家基弗于1953年首先提出的,70年代在中国推广。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |

![若有増根,则m的值是[]A.-2B.2C.3D.-3-八年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/85/2019-04-09/47ddc84666083f5bc2f5081659719228.gif)