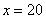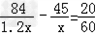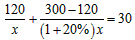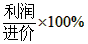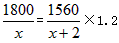已知某单位部分职工暑期去三爪仑漂流.现了解到下列信息:(1)三爪仑门票价格为50元/人,如果团体购票,人数超过25人,每增加1人,每张门票优惠1元,但每张门票不得低于35元.如-数学
题文
| 已知某单位部分职工暑期去三爪仑漂流.现了解到下列信息: (1)三爪仑门票价格为50元/人,如果团体购票,人数超过25人,每增加1人,每张门票优惠1元,但每张门票不得低于35元.如果该单位职工共支付门票费用1350元,请问该单位这次共有多少职工去三爪仑旅游? (2)在漂流时,职工小王口袋里恰好有3张人民币总共7元零钱.他请照相店的人拍了一些照片,他从中挑出了x张冲印,按标价应付y元,正好等于他那3张人民币中的2张面值之和,这时,相机里还有4张照片是小王没选的,店主便对小王说:“如果你把这剩下的也都冲印,那么连同刚才你冲印的,一共就付7元吧.”小王一算,这样相当于每张照片比标价减少了0.3元,本着互利的原则,小王便答应了.试求x和y值. |
答案
| (1)设这次共有x个去三爪仑旅游,依题意 ∵25×50=1250<1350, ∴x>25, 于是[50-(x-25)]?x=1350, 解得x1=30,x2=45, 当x2=45时,门票价格为50-(45-25)=30<35, 故x=30, 答:这次共有30人去三爪仑旅游. (2)3张人民币应分别为1元、1元、5元, 则y可能的取值为2或6, 依题意:当y=2时,
解得x为非整数解(舍), 当y=6时,
即3x2+22x-240=0,(3x+40)(x-6)=0, 解得x1=-
当x=6时,x(x+4)≠0, 故x=6,y=6. |
据专家权威分析,试题“已知某单位部分职工暑期去三爪仑漂流.现了解到下列信息:(1)三爪仑..”主要考查你对 分式方程的应用,一元二次方程的应用 等考点的理解。关于这些考点的“档案”如下:
分式方程的应用一元二次方程的应用
考点名称:分式方程的应用
列分式方程解应用题和列整式方程解应用题步骤基本相同,但必须注意,要检验求得的解是否为原方程的根,以及是否符合题意。
列分式方程解应用题的一般步骤是:
①找等量关系(审):理解题意,弄清具体情境中的已知量与未知量以及它们之间的基本关系;
②设:设未知数,用含x(或其他字母)表示某个未知数,由该未知数与其他数量的关系,写出表示相关量的式子;
③列:找出相等关系,列出分式方程;
④解:解这个分式方程;
⑤检验:双重检验,先检验是否为增根,再检验是否符合题意;
⑥答:写出答案。
例题
南宁到昆明西站的路程为828KM,一列普通列车和一列直达快车都从南宁开往昆明。直达快车的速度是普通快车速度的1.5倍,普通快车出发2H后,直达快车出发,结果比普通列车先到4H,求两次的速度.
设普通车速度是x千米每小时则直达车是1.5x
由题意得:
828/x-828/1.5x=6 ,
(828×1.5-828)/1.5x=6 ,
414/1.5=6x,
x=46, 1.5x=69
答:普通车速度是46千米每小时,直达车是69千米每小时。
无解的含义:
1.解为增根。
2.整式方程无解。(如:0x不等于0.)用分式解应用题的常见题型:
(1)行程问题有路程、时间和速度三个量,其关系式是路程=速度×时间,一般式以时间为等量关系。
(2)工程问题有工作效率、工作时间和工作总量三个量,其关系式是工作总量=工作效率×工作时间。
(3)增长率问题,其等量关系式是原量×(1+增长率)=增长后的量,原量×(1+减少率)=减少后的量。
考点名称:一元二次方程的应用
- 建立一元二次方程模型进行求解,把得到的答案带回实际问题中检验是否合理,来解决实际问题,如打折、营销、增长率问题等。
列一元二次次方程组解应用题的一般步骤:
可概括为“审、设、列、解、答”五步,即:
(1)审:是指读懂题意,弄清题意,明确哪些是已知量,哪些是未知量以及它们之间的关系;
(2)设:是指设未知数;
(3)列:就是列方程,这是非常重要的一步,一般先找出能够表达应用题全部含义的一个等量关系,然后列代数式表示等量关系中的各个量,就得到含有未知数的等式,即方程;
(4)解:解这个方程,求出两个未知数的值;
(5)答:在对求出的方程的解做出是否合理判断的基础上,写出答案。
提示:
①列方程解应用题时,要善于将普通语言化为数学语言,审题时,要特别注意关键词语,如“多、少、快、慢、和、差、倍、分、超过、剩余、增加、减少”等等,此外,还要掌握一些常用的公式或特殊的等量关系,如特殊图形的面积公式、行程问题、工程问题、增长率问题中的一些特殊关系等。
②注重解法选择与验根,在具体问题中要注意恰当的选择解法,以保证解题过程简单流畅,特别注意要对方程的解进行检验,根据实际情况作出正确取舍,以保证结论的准确性。
常见题型公式:
工程问题:
工程问题中的三个量及其关系为:工作总量=工作效率×工作时间
经常在题目中未给出工作总量时,设工作总量为单位1。利润赢亏问题
销售问题中常出现的量有:进价、售价、标价、利润等
有关关系式:
商品利润=商品售价—商品进价=商品标价×折扣率—商品进价
商品利润率=商品利润/商品进价
商品售价=商品标价×折扣率存款利率问题:
利息=本金×利率×期数
本息和=本金+利息
利息税=利息×税率(20%)行程问题:
基本数量关系:路程=速度×时间,时间=路程÷速度,速度=路程÷时间,
路程=速度×时间。
①相遇问题:快行距+慢行距=原距;
②追及问题:快行距-慢行距=原距;
③航行问题:顺水(风)速度=静水(风)速度+水流(风)速度,
逆水(风)速度=静水(风)速度-水流(风)速度
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |