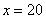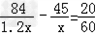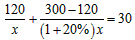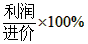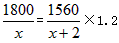题文

某工程队（有甲、乙两组）承包一条路段的修建工程，要求在规定时间内完成． （1）已知甲组单独完成这项工作所需时间比规定时间多32天，乙组单独完成这项工程所需时间比规定时间多12天，如果甲、乙两组先合作20天，剩下的由甲组单独做，则要误期2天完成，那么规定时间是多少天？ （2）在实际工作中，甲、乙两组合做这项工程的 5 6 后，工程队又承包了其他路段的工程，需抽调一组过去，从按时完成任务的角度考虑，你认为留下哪一组最好？请说明理由．

题型：解答题  难度：中档

答案

（1）设规定的时间是x天，根据题意得： x+2 x+32 + 20 x+12 =1， 解得x=28．经检验x=28是原方程的根， 答：规定的时间是28天． （2）设甲、乙两组合作完成这项工程的 5 6 用了y天，根据题意得： y（ 1 28+32 + 1 28+12 ）= 5 6 ， 解得：y=20， 若甲组单独做剩下的工程所需时间为（1- 5 6 ）÷ 1 28+32 =10（天）， ∵20+10=30＞28， ∴甲组单独做剩下的工程不能在规定的时间内完成． 若乙组单独做剩下的工程所需时间为（1- 5 6 ）÷ 1 28+12 = 20 3 =6 2 3 （天）， ∵20+6 2 3 =26 2 3 ＜28， ∴乙组单独做剩下的工程能在规定的时间内完成， ∴留下乙组最好．

据专家权威分析，试题“某工程队（有甲、乙两组）承包一条路段的修建工程，要求在规定时间..”主要考查你对  分式方程的应用  等考点的理解。关于这些考点的“档案”如下：

分式方程的应用

考点名称：分式方程的应用

• 列分式方程解应用题和列整式方程解应用题步骤基本相同，但必须注意，要检验求得的解是否为原方程的根，以及是否符合题意。
  列分式方程解应用题的一般步骤是：
  ①找等量关系（审）:理解题意,弄清具体情境中的已知量与未知量以及它们之间的基本关系;
  ②设:设未知数,用含x（或其他字母）表示某个未知数，由该未知数与其他数量的关系，写出表示相关量的式子；
  ③列：找出相等关系，列出分式方程；
  ④解：解这个分式方程；
  ⑤检验：双重检验，先检验是否为增根，再检验是否符合题意；
  ⑥答：写出答案。
  
  例题
  南宁到昆明西站的路程为828KM，一列普通列车和一列直达快车都从南宁开往昆明。直达快车的速度是普通快车速度的1.5倍,普通快车出发2H后，直达快车出发,结果比普通列车先到4H,求两次的速度.
  设普通车速度是x千米每小时则直达车是1.5x
  由题意得：
  828/x-828/1.5x=6 ，
  (828×1.5-828)/1.5x=6 ，
  414/1.5=6x，
  x=46, 1.5x=69
  答：普通车速度是46千米每小时，直达车是69千米每小时。
  
  无解的含义：
  1.解为增根。
  2.整式方程无解。（如：0x不等于0.）

• 用分式解应用题的常见题型：
  （1）行程问题有路程、时间和速度三个量，其关系式是路程=速度×时间，一般式以时间为等量关系。
  （2）工程问题有工作效率、工作时间和工作总量三个量，其关系式是工作总量=工作效率×工作时间。
  （3）增长率问题，其等量关系式是原量×（1+增长率）=增长后的量，原量×（1+减少率）=减少后的量。