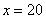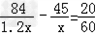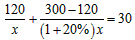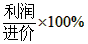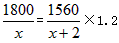注意:为了使同学们更好地解答本题,我们提供了一种解题思路,你可以依照这个思路按下面的要求填空,完成本题的解答.也可以选用其他的解题方案,此时不必填空,只需按照解答题-数学
题文
| 注意:为了使同学们更好地解答本题,我们提供了一种解题思路,你可以依照这个思路按下面的要求填空,完成本题的解答.也可以选用其他的解题方案,此时不必填空,只需按照解答题的一般要求进行解答. 方案一:甲队单独完成这项工程刚好能够如期完成; 方案二:乙队单独完成这项工程要比规定的时间多用10天; 方案三:若甲、乙两队合作8天,余下的由乙队单独做也正好如期完成. 又从甲、乙两个工程队的投标书中得知:每天需支付甲队的工程款1.5万元,乙队的工程款1.1万元. 试问,在不耽误工期的前提下,你觉得哪一种施工方案最节省工程款?请说明理由. 解题方案: 设甲队单独完成需x天,则乙队单独完成需(x+10)天. (1)用含x的代数式表示: 甲队每天可以完成这项工程的工作量是工程总量的______ 乙队每天可以完成这项工程的工作量是工程总量的______ 根据题意,列出相应方程______ 解这个方程,得______ 检验:______ (2)方案一得工程款为______; 方案二不合题意,舍去 方案三的工程款为______ 所以在不耽误工期的前提下,应选择方______能节省工程款. |
答案
| 设甲队单独完成需x天,则乙队单独完成需(x+10)天, 甲队可以完成这项工程的工作量是工程总量的
乙队可以完成这项工程的工作量是工程总量的
根据题意,列出相应方程得
解这个方程,得x=40, 经检验:x=40是原方程的根. (2)方案一得工程款为40×1.5=60(万元); 方案二不合题意,舍去; 方案三的工程款为8×1.5+40×1.1=56(万元); 所以在不耽误工期的前提下,应选择方案(3)能节省工程款. 故答案为:
|
据专家权威分析,试题“注意:为了使同学们更好地解答本题,我们提供了一种解题思路,你可..”主要考查你对 分式方程的应用 等考点的理解。关于这些考点的“档案”如下:
分式方程的应用
考点名称:分式方程的应用
列分式方程解应用题和列整式方程解应用题步骤基本相同,但必须注意,要检验求得的解是否为原方程的根,以及是否符合题意。
列分式方程解应用题的一般步骤是:
①找等量关系(审):理解题意,弄清具体情境中的已知量与未知量以及它们之间的基本关系;
②设:设未知数,用含x(或其他字母)表示某个未知数,由该未知数与其他数量的关系,写出表示相关量的式子;
③列:找出相等关系,列出分式方程;
④解:解这个分式方程;
⑤检验:双重检验,先检验是否为增根,再检验是否符合题意;
⑥答:写出答案。
例题
南宁到昆明西站的路程为828KM,一列普通列车和一列直达快车都从南宁开往昆明。直达快车的速度是普通快车速度的1.5倍,普通快车出发2H后,直达快车出发,结果比普通列车先到4H,求两次的速度.
设普通车速度是x千米每小时则直达车是1.5x
由题意得:
828/x-828/1.5x=6 ,
(828×1.5-828)/1.5x=6 ,
414/1.5=6x,
x=46, 1.5x=69
答:普通车速度是46千米每小时,直达车是69千米每小时。
无解的含义:
1.解为增根。
2.整式方程无解。(如:0x不等于0.)用分式解应用题的常见题型:
(1)行程问题有路程、时间和速度三个量,其关系式是路程=速度×时间,一般式以时间为等量关系。
(2)工程问题有工作效率、工作时间和工作总量三个量,其关系式是工作总量=工作效率×工作时间。
(3)增长率问题,其等量关系式是原量×(1+增长率)=增长后的量,原量×(1+减少率)=减少后的量。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |