如果第一次从1~4四个整数中任取出一个数,作为点P(m,n)的横坐标,第二次再从1~4四个整数中任取出一个数作为P(m,n)的纵坐标,得到点P(m,n).(1)试用列表或画树状图的方法列-数学
题文
| 如果第一次从1~4四个整数中任取出一个数,作为点P(m,n)的横坐标,第二次再从1~4四个整数中任取出一个数作为P(m,n)的纵坐标,得到点P(m,n). (1)试用列表或画树状图的方法列举出所有点P(m,n)的情形; (2)求出点P(m,n)在反比例函y=
|
题文
| 如果第一次从1~4四个整数中任取出一个数,作为点P(m,n)的横坐标,第二次再从1~4四个整数中任取出一个数作为P(m,n)的纵坐标,得到点P(m,n). (1)试用列表或画树状图的方法列举出所有点P(m,n)的情形; (2)求出点P(m,n)在反比例函y=
|
答案
(1)列表如下:
点P(m,n)共有16种可能的结果, 且每种结果出现的可能性相同, 点(1,4),(4,1),(2,2), 在反比例函数y=
故点P(m,n)在反比例函数y=
|
据专家权威分析,试题“如果第一次从1~4四个整数中任取出一个数,作为点P(m,n)的横坐标..”主要考查你对 反比例函数的图像,列举法求概率 等考点的理解。关于这些考点的“档案”如下:
反比例函数的图像列举法求概率
考点名称:反比例函数的图像

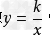 (k≠0),图像上一点P(x,y),作两坐标轴的垂线,两垂足、原点、P点组成一个矩形,矩形的面积
(k≠0),图像上一点P(x,y),作两坐标轴的垂线,两垂足、原点、P点组成一个矩形,矩形的面积 。过反比例函数过一点,作垂线,三角形的面积为
。过反比例函数过一点,作垂线,三角形的面积为 。
。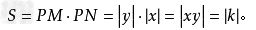
 存在两个交点,若设2点的横坐标分别为x1,x2,那么这两个交点与原点连线和两点之间的连线所构成的三角形面积为
存在两个交点,若设2点的横坐标分别为x1,x2,那么这两个交点与原点连线和两点之间的连线所构成的三角形面积为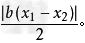

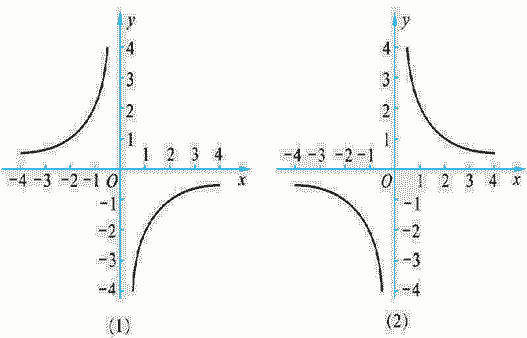
考点名称:列举法求概率
 。
。 | [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |