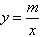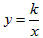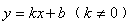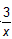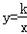题文

如图1，张老师设计了一个杠杆平衡条件的实验：在一个自制类似天平的仪器的左边固定托盘A中放置一个重物，在右边的活动托盘B（可左右移动）中放置一定质量的砝码，使得仪器左右平衡，改变活动托盘B与点O的距离x（cm），观察活动托盘B中砝码的质量y（g）的变化情况．实验数据记录如下表： x（cm） 10 15 20 25 30 y（g） 30 20 15 12 10 （1）把上表中（x，y）的各组对应值作为点的坐标，描在如图2所示的坐标系中，并用平滑的曲线将这些点连接起来； （2）观察所画的图象，猜测y与x之间的函数关系； （3）当砝码的质量为50g时，活动托盘B与点O的距离是多少？ （4）当活动托盘B往右移动时，应往活动托盘B中添加还是减少砝码？

题型：解答题  难度：中档

答案

（1）如图所示： （2）由图象猜测y与x之间的函数关系为反比例函数， ∴设y= k x （k≠0）， 把x=10，y=30代入得：k=300， ∴y= 300 x ， 将其余各点代入验证均适合， ∴y与x的函数关系式为：y= 300 x ． （3）把y=50代入y= 300 x 得：x=6， ∴当砝码的质量为50g时，活动托盘B与点O的距离是6cm． （4）根据反比例函数的增减性，即可得出，随着活动托盘B与O点的距离不断增大，砝码的示数会不断减小； ∴应减少砝码．

据专家权威分析，试题“如图1，张老师设计了一个杠杆平衡条件的实验：在一个自制类似天平..”主要考查你对  求反比例函数的解析式及反比例函数的应用  等考点的理解。关于这些考点的“档案”如下：

求反比例函数的解析式及反比例函数的应用

考点名称：求反比例函数的解析式及反比例函数的应用

• 反比例函数解析式的确定方法：
  由于在反比例函数关系式 ：y= 中，只有一个待定系数k，确定了k的值，也就确定了反比例函数。因此，只需给出一组x、y的对应值或图象上一点的坐标，代入中即可求出k的值，从而确定反比例函数的关系式。但在实际求反比例函数的解析式时，应该具体问题具体分析。

  反比例函数的应用：
  建立函数模型，解决实际问题。

• 用待定系数法求反比例函数关系式的一般步骤是：
  ①设所求的反比例函数为：y= (k≠0)；
  ②根据已知条件（自变量与函数的对应值）列出含k的方程；
  ③由代人法解待定系数k的值；
  ④把k值代人函数关系式y= 中。
  
  反比例函数应用一般步骤：
  ①审题；
  ②求出反比例函数的关系式；
  ③求出问题的答案，作答。