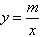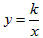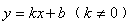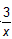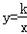题文

如图，是一辆小汽车沿一条高速公路匀速前进的时间y（小时）与速度x（千米/时）关系的图象，根据图象提供的信息，解答下列问题： （1）这条公路的全长是多少千米； （2）写出速度与时间之间的函数关系式； （3）汽车最大速度可以达到多少； （4）汽车最慢用几个小时可以达到？如果要在3小时内达到，汽车的速度应不少于多少？

题型：解答题  难度：中档

答案

（1）以150千米/时行驶了两小时，则路程=150×2=300千米． （2）由速度= 路程 时间 ，路程为300千米，则有y= 300 x ； （3）据图象用1小时可以行驶完全程，所以汽车最大速度可以达到300千米/小时； （4）据图象，最低速度为50千米/小时，需要6时行完全程，汽车的速度应不少于每小时100千米．

据专家权威分析，试题“如图，是一辆小汽车沿一条高速公路匀速前进的时间y（小时）与速度x..”主要考查你对  求反比例函数的解析式及反比例函数的应用  等考点的理解。关于这些考点的“档案”如下：

求反比例函数的解析式及反比例函数的应用

考点名称：求反比例函数的解析式及反比例函数的应用

• 反比例函数解析式的确定方法：
  由于在反比例函数关系式 ：y= 中，只有一个待定系数k，确定了k的值，也就确定了反比例函数。因此，只需给出一组x、y的对应值或图象上一点的坐标，代入中即可求出k的值，从而确定反比例函数的关系式。但在实际求反比例函数的解析式时，应该具体问题具体分析。

  反比例函数的应用：
  建立函数模型，解决实际问题。

• 用待定系数法求反比例函数关系式的一般步骤是：
  ①设所求的反比例函数为：y= (k≠0)；
  ②根据已知条件（自变量与函数的对应值）列出含k的方程；
  ③由代人法解待定系数k的值；
  ④把k值代人函数关系式y= 中。
  
  反比例函数应用一般步骤：
  ①审题；
  ②求出反比例函数的关系式；
  ③求出问题的答案，作答。