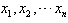下列说法正确的是()A.一个游戏的中奖概率是15,则做5次这样的游戏一定会中奖B.一组数据6,8,6,8,8,9,10的众数和中位数都是8C.为了了解一批电视机的使用寿命,应该采取普-数学
题文
下列说法正确的是( )
|
答案
A、一个游戏的中奖概率是
B、一组数据6,8,6,8,8,9,10的众数和中位数都是8,正确; C、为了了解一批电视机的使用寿命,应该采取抽样调查的方式,故本选项错误; D、若甲组数据的方差S甲2=0.02,乙组数据的方差差S乙2=0.2.则甲组数据比甲组数据稳定,故本选项错误. 故选B. |
据专家权威分析,试题“下列说法正确的是()A.一个游戏的中奖概率是15,则做5次这样的游戏..”主要考查你对 中位数和众数,方差,概率的意义,全面调查和抽样调查 等考点的理解。关于这些考点的“档案”如下:
中位数和众数方差概率的意义全面调查和抽样调查
考点名称:中位数和众数
- 中位数:一般地,n个数据按大小顺序排列,处于最中间位置的一个数据(或最中间位置的两个数据的平均数)叫这组数据的中位数。
众数:在一组数据中,出现次数最多的数据。 - 中位数的位置:
当样本数为奇数时,中位数=(N+1)/2;当样本数为偶数时,中位数为N/2与1+N/2的均值
众数性质:
用众数代表一组数据,可靠性较差,不过,众数不受极端数据的影响,并且求法简便。在一组数据中,如果个别数据有很大的变动,选择中位数表示这组数据的“集中趋势”就比较适合。
当数值或被观察者没有明显次序(常发生于非数值性资料)时特别有用,由于可能无法良好定义算术平均数和中位数。例子:{鸡、鸭、鱼、鱼、鸡、鱼}的众数是鱼。
众数算出来是销售最常用的,代表最多的
众数是在一组数据中,出现次数最多的数据
两组数据中,都是1,2出现次数最多
所以1,2是众数
众数:
一般来说,一组数据中,出现次数最多的数就叫这组数据的众数。
例如:1,2,3,3,4的众数是3。
但是,如果有两个或两个以上个数出现次数都是最多的,那么这几个数都是这组数据的众数。
例如:1,2,2,3,3,4的众数是2和3。
还有,如果所有数据出现的次数都一样,那么这组数据没有众数。
例如:1,2,3,4,5没有众数。
在高斯分布中,众数位于峰值。
平均数、中位数和众数的特征:
(1)平均数、中位数、众数都是表示一组数据“平均水平”的平均数。
(2)平均数能充分利用数据提供的信息,在生活中较为常用,但它容易受极端数字的影响,且计算较繁。
(3)中位数的优点是计算简单,受极端数字影响较小,但不能充分利用所有数字的信息。 中位数算出来可避免极端数据,代表着数据总体的中等情况。
(4)众数的可靠性较差,它不受极端数据的影响,求法简便,当一组数据中个别数据变动较大时,适宜选择众数来表示这组数据的“集中趋势”。 平均数、中位数和众数异同:
一、相同点
平均数、中位数和众数这三个统计量的相同之处主要表现在:都是来描述数据集中趋势的统计量;都可用来反映数据的一般水平;都可用来作为一组数据的代表。
二、不同点
它们之间的区别,主要表现在以下方面。
1、定义不同
平均数:一组数据的总和除以这组数据个数所得到的商叫这组数据的平均数。
中位数:将一组数据按大小顺序排列,处在最中间位置的一个数叫做这组数据的中位数 。
众数:在一组数据中出现次数最多的数叫做这组数据的众数。
2、求法不同
平均数:用所有数据相加的总和除以数据的个数,需要计算才得求出。
中位数:将数据按照从小到大或从大到小的顺序排列,如果数据个数是奇数,则处于最中间位置的数就是这组数据的中位数;如果数据的个数是偶数,则中间两个数据的平均数是这组数据的中位数。它的求出不需或只需简单的计算。
众数:一组数据中出现次数最多的那个数,不必计算就可求出。
3、个数不同
在一组数据中,平均数和中位数都具有惟一性,但众数有时不具有惟一性。在一组数据中,可能不止一个众数,也可能没有众数。
4、呈现不同
平均数:是一个“虚拟”的数,是通过计算得到的,它不是数据中的原始数据。
中位数:是一个不完全“虚拟”的数。当一组数据有奇数个时,它就是该组数据排序后最中间的那个数据,是这组数据中真实存在的一个数据;但在数据个数为偶数的情况下,中位数是最中间两个数据的平均数,它不一定与这组数据中的某个数据相等,此时的中位数就是一个虚拟的数。
众 数:是一组数据中的原数据 ,它是真实存在的。
5、代表不同
平均数:反映了一组数据的平均大小,常用来一代表数据的总体 “平均水平”。
中位数:像一条分界线,将数据分成前半部分和后半部分,因此用来代表一组数据的“中等水平”。
众数:反映了出现次数最多的数据,用来代表一组数据的“多数水平”。
这三个统计量虽反映有所不同,但都可表示数据的集中趋势,都可作为数据一般水平的代表。
6、特点不同
平均数:与每一个数据都有关,其中任何数据的变动都会相应引起平均数的变动。主要缺点是易受极端值的影响,这里的极端值是指偏大或偏小数,当出现偏大数时,平均数将会被抬高,当出现偏小数时,平均数会降低。
中位数:与数据的排列位置有关,某些数据的变动对它没有影响;它是一组数据中间位置上的代表值,不受数据极端值的影响。
众数:与数据出现的次数有关,着眼于对各数据出现的频率的考察,其大小只与这组数据中的部分数据有关,不受极端值的影响,其缺点是具有不惟一性,一组数据中可能会有一个众数,也可能会有多个或没有 。
7、作用不同
平均数:是统计中最常用的数据代表值,比较可靠和稳定,因为它与每一个数据都有关,反映出来的信息最充分。平均数既可以描述一组数据本身的整体平均情况,也可以用来作为不同组数据比较的一个标准。因此,它在生活中应用最广泛,比如我们经常所说的平均成绩、平均身高、平均体重等。
中位数:作为一组数据的代表,可靠性比较差,因为它只利用了部分数据。但当一组数据的个别数据偏大或偏小时,用中位数来描述该组数据的集中趋势就比较合适。
众数:作为一组数据的代表,可靠性也比较差,因为它也只利用了部分数据。。在一组数据中,如果个别数据有很大的变动,且某个数据出现的次数最多,此时用该数据(即众数)表示这组数据的“集中趋势”就比较适合。- 中位数、众数的求法:
中位数:
①将数据按大小顺序排列;
②当数据个数为奇数时,中间的那个数据就是中位数;
当数据个数为偶数时,居于中间的两个数据的平均数才是中位数。
众数:找出频数最多的数据,若几个数据频数最多且相同,此时众数就是这几个数据。
考点名称:方差
- 方差:
是各个数据与平均数之差的平方和的平均数。
在概率论和数理统计中,方差用来度量随机变量和其数学期望(即均值)之间的偏离程度。
在许多实际问题中,研究随机变量和均值之间的偏离程度有着很重要的意义。
设有n个数据各数据x1,x2,…,xn各数据与它们的平均数的差的平方分别是 ,
, ,…,
,…, ,我们用它的平均数,即用
,我们用它的平均数,即用 来衡量这组数据的波动大小,并把它叫做这组数据的方差,记作
来衡量这组数据的波动大小,并把它叫做这组数据的方差,记作 。
。 - 方差特点:
(1)设c是常数,则D(c)=0。
(2)设X是随机变量,c是常数,则有D(cX)=(c2)D(X)。
(3)设 X 与 Y 是两个随机变量,则
D(X+Y)= D(X)+D(Y)+2E{[X-E(X)][Y-E(Y)]}
特别的,当X,Y是两个相互独立的随机变量,上式中右边第三项为0(常见协方差),
则D(X+Y)=D(X)+D(Y)。此性质可以推广到有限多个相互独立的随机变量之和的情况。
(4)D(X)=0的充分必要条件是X以概率为1取常数值c,即P{X=c}=1,其中E(X)=c。
(5)D(aX+bY)=a^2DX+b^2DY+2abE{[X-E(X)][Y-E(Y)]}。
意义:
在样本容量相同的情况下,方差越大,说明数据的波动越大,越不稳定。
标准差:
方差的算术平均根,即 ,并把它叫做这组数据的标准差,它也是一个用来衡量一组数据的波动大小的重要的量。
,并把它叫做这组数据的标准差,它也是一个用来衡量一组数据的波动大小的重要的量。 公式:
方差是实际值与期望值之差平方的期望值,而标准差是方差算术平方根。 在实际计算中,我们用以下公式计算方差。
方差是各个数据与平均数之差的平方的平均数,即s^2=(1/n)[(x1-x_)^2+(x2-x_)^2+...+(xn-x_)^2],其中,x_表示样本的平均数,n表示样本的数量,^,xn表示个体,而s^2就表示方差。
而当用(1/n)[(x1-x_)^2+(x2-x_)^2+...+(xn-x_)^2]作为样本X的方差的估计时,发现其数学期望并不是X的方差,而是X方差的(n-1)/n倍,[1/(n-1)][(x1-x_)^2+(x2-x_)^2+...+(xn-x_)^2]的数学期望才是X的方差,用它作为X的方差的估计具有“无偏性”,所以我们总是用[1/(n-1)]∑(xi-X~)^2来估计X的方差,并且把它叫做“样本方差”。
方差,通俗点讲,就是和中心偏离的程度!用来衡量一批数据的波动大小(即这批数据偏离平均数的大小)并把它叫做这组数据的方差。记作S².在样本容量相同的情况下,方差越大,说明数据的波动越大,越不稳定。
方差分析主要用途:
①均数差别的显著性检验;
②分离各有关因素并估计其对总变异的作用;
③分析因素间的交互作用;
④方差齐性检验。
考点名称:概率的意义
- 概率的意义:
一般地,在大量重复试验中,如果事件A发生的频率 会稳定在某个常数p附近,那么这个常数p就叫做事件A的概率,记作P(A)=p,概率从某种数量上刻画一个不确定事件发生的可能性的大小。
会稳定在某个常数p附近,那么这个常数p就叫做事件A的概率,记作P(A)=p,概率从某种数量上刻画一个不确定事件发生的可能性的大小。
事件和概率的表示方法:一般地,事件用英文大写字母A,B,C,…,表示事件A的概率p,可记为P(A)=P。
事件的概率:必然事件的概率为1,不可能事件的概率为0,随机事件A的概率为0<P(A)<1。
注:(1)在n试验中,事件A发生的频率m满足0≤m≤n,所以0≤ ≤1,故0≤P(A)≤1;
≤1,故0≤P(A)≤1;
(2)P(A)=0表示事件A是不可能发生的事件,P(A)=1表示事件A是必然发生的事件;
(3)概率越大,表示事件发生的可能性越大;概率越小,表示事件发生的可能性越小;
(4)人们通常对随机事件进行大量的反复试验来研究概率,一般大量试验事件发生的频率可作为概率的估计值。
考点名称:全面调查和抽样调查
- 全面调查:
就是对需要调查的对象进行逐个调查。这种方法所得资料较为全面可靠,但调查花费的人力、物力、财力较多,且调查时间较长,不适合一般企业的要求。全面调查只在产品销售范围很窄或用户很少的情况下可以采用。对品种多、产量大、销售范围广的产品,就不适用全面调查,而可以采用抽样调查。
抽样调查:
是从需要调查对象的总体中,抽取若干个个体即样本进行调查,并根据调查的情况推断总体的特征的一种调查方法。
抽样调查可以把调查对象集中在少数样本上,并获得与全面调查相近的结果。这是一种较经济的调查方法,因而被广泛采用。抽样调查是从研究对象的总体中抽取一部分个体作为样本进行调查,据此推断有关总体的数字特征。 调查好处与特点:
1.全面调查:对需要调查的对象进行逐个调查。
好处:所得资料较为全面可靠。
特点:调查花费的人力、物力、财力较多,且调查时间较长,全面调查只在样本很少的情况下适合采用。2.抽样调查:是一种非全面调查,它是从全部调查研究对象中,抽选一部分单位进行调查,并据以对全部调查研究对象作出估计和推断的一种调查方法。
好处:耗费的人力,物力,财力少,大量节约调查时间。
特点:
1、按随机原则抽选样本。
2、总体中每一个单位都有一定的概率被抽中。
3、可以用一定的概率来保证将误差控制在规定的范围之内。
4、适合样本数量较多的情况下采用。- 全面调查和抽样调查关系:
全面调查和抽样调查是按调查对象范围不同划分的调查方式。
全面调查是对调查对象中的所有单位全部加以调查,通过基层单位按照一定的报表填报要求进行逐一登记、逐级上报、层层汇总,最后取得调查结果的一种调查方式,如人口普查、经济普查等。
抽样调查是一种非全面调查,它是从研究的总体中按随机原则抽取部分样本单位进行调查,并根据样本单位的调查结果来推断总体,以达到认识总体的一种统计调查方式。
抽样调查用样本指标代表总体指标不可避免会产生误差,抽样推断虽然会有抽样误差(不包括登记误差和系统性误差),但只要严格遵守随机原则,所选的样本结构与总体结构相同,或者两者分布一致,就可以运用数学公式计算抽样误差。随机抽样产生的误差,只要确定其具体的数量界限,可以通过抽样程序设计加以控制。因此抽样调查的结果是有可靠的科学依据的。
抽样调查与全面调查有着相辅相成的关系。在实际运用中,没有必要进行全面调查和不可能进行全面调查时宜采用抽样调查。
抽样调查的优点:
一是由于只从总体中抽取一部分样本进行调查,工作量小,所以比全面调查节省人力、物力、财力,比较经济;
二是可以及时取得调查资料,提高数据的时效性;
三是数据质量有保证,由于抽样调查一般是自上而下组织调查,直接派员深入实际抽取样本并推断总体,可以减少人为因素干扰,只要取样、推断方法科学,均有利于提高数据的质量;
第四,调查方法灵活,如实际工作中使用较多的问卷调查、入户调查、电话调查等,适应面广,特别适于对点多面广的总体作调查。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |

![某班甲、乙两组模拟考成绩的盒状图如图所示.若甲、乙两组模拟考成绩的极差分别为a、b;中位数分别为c、d,则a、b、c、d的大小关系,下列何者正确?[]A.a<b且c>dB.a&l-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/93/2019-04-14/1763e86cc602affc40dfc9e351d9321a.png)
![在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如下表:这些运动员跳高成绩的中位数和众数分别是[]A.1.65,1.70B.1.70,1.65C.1.70,1.70D.3,5-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/93/2019-04-14/c325d134726e734a0c45ba6bbc3c3878.gif)
![为了了解某校2009年初三学生体育测试成绩,从中随机抽取了50名学生的体育测试成绩如下表:则这50名学生的体育测试成绩的众数、中位数分别为[]A.24,24B.8,24C.24,23.5D-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/93/2019-04-14/7e67304eabdffa90f75b3e96c4119112.gif)
![某电脑公司试销同一价位的品牌电脑,一周内销售情况如下表所示:要了解哪种品牌最畅销,公司经理最关心的是上述数据找[]A.平均数B.众数C.中位数D.方差-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/93/2019-04-14/af758fef114f1a7fa00ccb52dc0427e4.gif)