某体校为了选拔一名射击运动员参加一项市级比赛,对甲、乙两名射击运动员进行了10次选拔比赛,他们的成绩(单位:环)如下:甲:7868558968乙:9578768677(1)甲、乙两名运动员射击-数学
题文
| 某体校为了选拔一名射击运动员参加一项市级比赛,对甲、乙两名射击运动员进行了10次选拔比赛,他们的成绩(单位:环)如下: 甲:7868558968 乙:9578768677 (1)甲、乙两名运动员射击的平均成绩分别是多少? (2)哪个人的射击成绩更为稳定? (3)经预测,命中8环,就可能获得冠军,该体校为了获取射击的冠军,可能选择哪位运动员参赛?为什么? (计算方差的公式:S2=
|
答案
(1)甲、乙两人射击成绩的平均成绩分别为:
(2)
∵s甲2>s乙2. ∴乙同学的射击成绩比较稳定. (3)∵经预测,命中8环,就可能获得冠军,根据甲同学获得8环以上的成绩较多, ∴应该派甲同学参加比赛. |
据专家权威分析,试题“某体校为了选拔一名射击运动员参加一项市级比赛,对甲、乙两名射..”主要考查你对 方差 等考点的理解。关于这些考点的“档案”如下:
方差
考点名称:方差
- 方差:
是各个数据与平均数之差的平方和的平均数。
在概率论和数理统计中,方差用来度量随机变量和其数学期望(即均值)之间的偏离程度。
在许多实际问题中,研究随机变量和均值之间的偏离程度有着很重要的意义。
设有n个数据各数据x1,x2,…,xn各数据与它们的平均数的差的平方分别是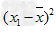 ,
,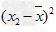 ,…,
,…, ,我们用它的平均数,即用
,我们用它的平均数,即用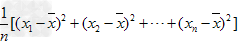 来衡量这组数据的波动大小,并把它叫做这组数据的方差,记作
来衡量这组数据的波动大小,并把它叫做这组数据的方差,记作 。
。 - 方差特点:
(1)设c是常数,则D(c)=0。
(2)设X是随机变量,c是常数,则有D(cX)=(c2)D(X)。
(3)设 X 与 Y 是两个随机变量,则
D(X+Y)= D(X)+D(Y)+2E{[X-E(X)][Y-E(Y)]}
特别的,当X,Y是两个相互独立的随机变量,上式中右边第三项为0(常见协方差),
则D(X+Y)=D(X)+D(Y)。此性质可以推广到有限多个相互独立的随机变量之和的情况。
(4)D(X)=0的充分必要条件是X以概率为1取常数值c,即P{X=c}=1,其中E(X)=c。
(5)D(aX+bY)=a^2DX+b^2DY+2abE{[X-E(X)][Y-E(Y)]}。
意义:
在样本容量相同的情况下,方差越大,说明数据的波动越大,越不稳定。
标准差:
方差的算术平均根,即 ,并把它叫做这组数据的标准差,它也是一个用来衡量一组数据的波动大小的重要的量。
,并把它叫做这组数据的标准差,它也是一个用来衡量一组数据的波动大小的重要的量。 公式:
方差是实际值与期望值之差平方的期望值,而标准差是方差算术平方根。 在实际计算中,我们用以下公式计算方差。
方差是各个数据与平均数之差的平方的平均数,即s^2=(1/n)[(x1-x_)^2+(x2-x_)^2+...+(xn-x_)^2],其中,x_表示样本的平均数,n表示样本的数量,^,xn表示个体,而s^2就表示方差。
而当用(1/n)[(x1-x_)^2+(x2-x_)^2+...+(xn-x_)^2]作为样本X的方差的估计时,发现其数学期望并不是X的方差,而是X方差的(n-1)/n倍,[1/(n-1)][(x1-x_)^2+(x2-x_)^2+...+(xn-x_)^2]的数学期望才是X的方差,用它作为X的方差的估计具有“无偏性”,所以我们总是用[1/(n-1)]∑(xi-X~)^2来估计X的方差,并且把它叫做“样本方差”。
方差,通俗点讲,就是和中心偏离的程度!用来衡量一批数据的波动大小(即这批数据偏离平均数的大小)并把它叫做这组数据的方差。记作S².在样本容量相同的情况下,方差越大,说明数据的波动越大,越不稳定。
方差分析主要用途:
①均数差别的显著性检验;
②分离各有关因素并估计其对总变异的作用;
③分析因素间的交互作用;
④方差齐性检验。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |

![甲、乙两中学生在一年里学科平均分相等,但他们的方差不相等,下列对他们学习情况的评价正确的是[]A.因为他们的平均分相等,所以学习水平一样B.成绩虽然一样,方差较大的,说-八年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/95/2019-04-16/2cb2de79eef83370fbd4f4e947e1609c.png)
![一个样本的方差是s2=[(x1-8)2+(x2-8)2+…+(x10-8)2],则这个样本数据的个数是(),样本平均数是()。-八年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/95/2019-04-16/43a2c555bd880098742701a3536138f7.gif)
![10名同学分成甲、乙两队进行篮球比赛,他们的身高(单位:cm)如下表所示:[]A.,;B.,C.,D.,-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/95/2019-04-16/dbb57e9c63a2d7d6eb51e6b4677b5a25.png)
![下列说法正确的是[]A.为了检验一批零件的质量,从中抽取10件,在这个问题中,10是抽取的样本B.如果x1、x2、.….xn的平均数是,那么(x1-)+(x1-)+…+(xn-)=0C.8、9、10、11-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/95/2019-04-16/d0cb3102870e7039bed261be130598bd.png)
