有一块边长是10分米的正方形木板,把它锯成一个尽可能大的圆板,面积减少了百分之几?-六年级数学
题文
| 有一块边长是10分米的正方形木板,把它锯成一个尽可能大的圆板,面积减少了百分之几? |
答案
| [10×10-3.14×(10÷2)2]÷(10×10)×100%=21.5% |
据专家权威分析,试题“有一块边长是10分米的正方形木板,把它锯成一个尽可能大的圆板,..”主要考查你对 百分数的计算,百分数的应用题,正方形的面积,圆的面积 等考点的理解。关于这些考点的“档案”如下:
百分数的计算,百分数的应用题正方形的面积圆的面积
考点名称:百分数的计算,百分数的应用题
- 常见的百分数的计算方法:

- 百分数应用题关系式:
利息的计算公式:利息=本金×利率×时间。
百分率:例:发芽率=发芽种子数÷试验种子数×100%
利率=利息÷本金×100%
折数=现价÷原价
成数=实际收成÷计划收成
税率=应纳税额÷总收入×100%
利润=售出价-成本,利润率=利润÷成本×100%=(售出价÷成本-1)×100%
折扣=实际售价÷原售价×100%(折扣<1)
浓度问题:
溶质的重量+溶剂的重量=溶液的重量;
溶质的重量÷溶液的重量×100%=浓度;
溶液的重量×浓度=溶质的重量;
溶质的重量÷浓度=溶液的重量。
考点名称:正方形的面积
- 学习目标:
理解掌握正方形面积计算公式,并且会运用公式进行计算。 - 面积公式:
正方形面积=边长×边长,用字母表示:S=a×a=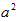 。
。
考点名称:圆的面积
- 圆的面积公式:
圆的面积=半径×半径×圆周率;
S=π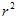 (r—半径,d—直径,π—圆周率)
(r—半径,d—直径,π—圆周率)
圆环面积:
外圆面积-内圆面积;
S=π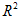 -π
-π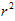 =π(
=π( -
-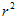 )(R—外圆半径,r—内圆半径)
)(R—外圆半径,r—内圆半径)
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:“十一”黄金周期间,爸爸与小明一起去旅游,实际消费金额比原计划节约了25%,他们原计划消费金额比实际消费多百分之几?-六年级数学
下一篇:新潮玩具厂去年总产值是125万元,超过原计划25万元。产值增加了百分之几?-六年级数学
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |

