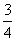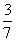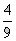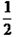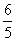一种什锦糖是巧克力、水果糖、奶糖按照2:3:5配制而成.(1)如果要配制120千克这样什锦糖,那么这三种糖各需多少千克?(2)三种糖现各有30千克,那么配制上述什锦糖时,当水果糖用-数学
题文
| 一种什锦糖是巧克力、水果糖、奶糖按照2:3:5配制而成. (1)如果要配制120千克这样什锦糖,那么这三种糖各需多少千克? (2)三种糖现各有30千克,那么配制上述什锦糖时,当水果糖用完后,奶糖应增加多少千克?巧克力还剩多少千克? |
答案
| (1)总份数:2+3+5=10(份), 巧克力的数量:120×
水果糖的数量:120×
奶糖的数量:120×
答:如果要配制120千克这样什锦糖,那么这三种糖各需24千克,36千克,60千克. (2)什锦糖的数量: 30÷
奶糖的数量:100×
奶糖应增加的数量:50-30=20(千克), 巧克力的数量:100×
巧克力剩的数量:30-20=10(千克). 答:当水果糖用完后,奶糖应增加20千克,巧克力还剩10千克. |
据专家权威分析,试题“一种什锦糖是巧克力、水果糖、奶糖按照2:3:5配制而成.(1)如果要配..”主要考查你对 解比例,比例的应用题 等考点的理解。关于这些考点的“档案”如下:
解比例,比例的应用题
考点名称:解比例,比例的应用题
解比例:
求比例中的未知项,叫做解比例。
根据比例的基本性质(即交叉相乘),如果已知比例中的任何三项,就可以求出这个比例中的另外一个未知项。求比例中的未知项,叫做解比例。解比例是利用比例的基本性质:在比例中,两个外项的积等于两个内项的积。再转化成方程。
比例应用题:
是小学六年级奥数中的一个重要内容。它既是整数应用题的继续与深化,又是学习更多数学知识的重要基础,同时,这类题又有着自身的特点和解题的规律。在处理几个量的倍比关系时,比例应用题与分数百分数应用题间有很多相似之处,但利用比例处理问题要方便灵活得多。
要解决好此类问题,须注意灵活运用画线段示意图等手段,多角度、多侧面思考问题。在解题过程中,要善于掌握对应、假设、转化等多种解题方法,在寻找正确的解题方法的同时,不断地开拓解题思路。- 用比例方法解应用题的一般步骤:

- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |